A liofilização é um processo de desidratação de alimentos que, além de evitar que seus nutrientes saiam junto com a água, diminui bastante sua massa e seu volume, facilitando o armazenamento e o transporte. Alimentos liofilizados também têm seus prazos de validade aumentados, sem perder características como aroma e sabor.

O processo de liofilização segue as seguintes etapas:
I. O alimento é resfriado até temperaturas abaixo de 0 ºC, para que a água contida nele seja solidificada.
II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada. Dessa forma, a água sai do alimento sem romper suas estruturas moleculares, evitando perdas de proteínas e vitaminas.
O gráfico mostra parte do diagrama de fases da água e cinco processos de mudança de fase, representados pelas setas numeradas de 1 a 5.
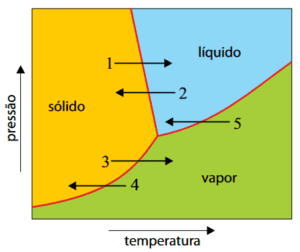
A alternativa que melhor representa as etapas do processo de liofilização, na ordem descrita, é
(A) 4 e 1.
(B) 2 e 1.
(C) 2 e 3.
(D) 1 e 3.
(E) 5 e 3.
Solução:
Na primeira etapa, a água passa do estado líquido para o estado sólido, portanto é o processo 2. Na segunda etapa, a água passa do estado sólido diretamente para o estado de vapor, portanto é o processo 3.
Resposta: letra C.



