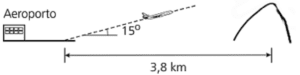
Ao decolar, um avião deixa o solo com um ângulo constante de 15º. A 3,8 km da cabeceira da pista existe um morro íngreme. A figura abaixo ilustra a decolagem, fora de escala. Podemos concluir que o avião ultrapassa o morro a uma altura, a partir da sua base, de
a) 3,8 tan (15°) km.
b) 3,8 sen (15°) km.
c) 3,8 cos (15°) km.
d) 3,8 sec (15°) km.
Solução:
Utilizando as relações trigonométricas do triângulo retângulo, nota-se, pela figura abaixo, que a distância entre o ponto de decolagem e o morro é o cateto adjacente ao ângulo de 15º, enquanto que a altura $$(h)$$ atingida pelo voo é o cateto oposto do triângulo retângulo em questão.
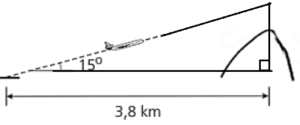
Desse modo, $$tg(15^{0})=\frac{h}{3,8}\Longrightarrow h =3,8\cdot tg(15^{0}) Km$$.
Resposta: a)





