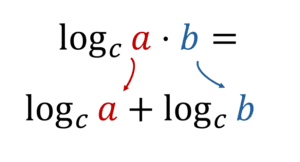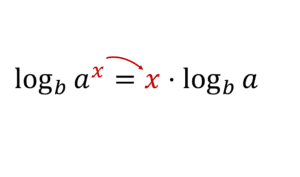QuestãoSendo c um número real, considere a função afim $$f(x)=2x+c$$ , definida para todo número real ?.
a) Encontre todas as soluções da equação $$[f(x)]^{3}=f(x^{3})$$, para c = 1.
b) Determine todos os valores de ? para os quais a função $$g(x)=log(x\cdot f(x)+c)$$ esteja definida para todo número real x.
Solução:
a) Fazendo $$(2x+1)^{3}=2x^{3}+1$$, obtemos $$6x(x^{2}+2x+1)=0$$. Pondo $$x=0$$, teremos uma solução para a equação. A outra virá por Bhaskara na equação de dentro dos parênteses.
\[x=\frac{-2\pm\sqrt{4-4}}{2}=\frac{-2}{2}=-1\].
Os valores são $$x=0$$ ou $$x=-1$$.
b) Utilizando a condição de existência do logaritmo a qual nos impõe o logaritmando não nulo, temos $$x(2x+c)+c\neq 0 \Longrightarrow 2x^{2}+cx+x\neq 0$$.
A fim de que esta equação não tenha solução real para todo $$x$$, teremos de indicar os valores de $$c$$ para os quais a raiz quadrada não existe, ou seja, para que o o radicando seja inferior a 0.
\[c^{2}-8c<0\].
Esta parábola possui concavidade voltada para cima. Suas raízes são $$c=0$$ e $$c=8$$. Portanto o intervalo de $$c$$ em que a inequação é negativa só pode ser $$0<c<8$$. Este intervalo garante que o logaritmo exista para todo $$x$$.
Resolução – UNICAMP 2018 – 2ª Fase – Q 14 (Matemática)