As equações de 2º grau incompletas são aquelas que não possuem todos os coeficientes diferentes de zero. Considere que uma equação do segundo grau sempre terá a forma ax²+bx+c=0.
🔸 1º FORMA: c=0
A equação incompleta nesta forma será $$ax^{2}+bx=0$$, pois o termo independente (c) é igual a zero. Para resolver a equação nesta forma, basta fatorar o ‘x’: $$ax^{2}+bx = x(ax+b) = 0$$. Isso faz com que tenhamos duas soluções: $$x=0$$ ou $$ax+b=0$$, esta última equivale a dizer que $$x=-\frac{b}{a}.$$
As duas soluções serão sempre $$\mathbf{x=0}$$ ou $$\mathbf{x=-(b/a)}$$.
Exemplo: $$2x^{2}+11x=0$$.
Se fizermos a fatoração, teremos $$x(2x+11)=0$$, então $$x=0$$ ou $$x=-11/2$$.
Para aplicar a fórmula apresentada, basta notar que $$a=2, b=11$$ e $$c=0$$, logo teremos sempre $$x=0$$ ou $$x=-11/2$$.
Exemplo: $$-x + 3x^{2}=0$$.
Os termos apenas estão invertidos, isso quer dizer que $$a=3$$ e $$b=-1$$. As soluções serão $$x=0$$ ou $$x=-(-1/3) = 1/3$$.
Confira, no vídeo ao lado, nossa explicação e mais exemplos numéricos sobre a 1ª forma das equações incompletas de segundo grau.
🔸 2ª FORMA: b = 0
Neste caso, sempre teremos $$ax^{2}+c=0$$. Mas tenha atenção, pois os sinais de $$a$$ e $$c$$ sempre devem ser diferentes (se um é positivo, o outro tem de ser negativo!), a fim de que não apareça a temida raiz quadrada de número negativo! Dito isso, a nossa solução sempre será $$x=\sqrt{-a/b}$$ ou $$x=-\sqrt{-a/b}$$.
Exemplo: $$-x^{2} + 3=0$$.
Teremos $$-x^{2}=-3$$, então $$x=\pm\sqrt{3}$$.
Para aplicarmos a fórmula, basta observar que $$a=-1$$ e $$c=3$$, logo $$x=\pm\sqrt{-(-1/3)}=\pm\sqrt{1/3}$$.
Confira, no vídeo ao lado, nossa explicação e mais exemplos numéricos sobre a 2ª forma das equações incompletas de segundo grau.
















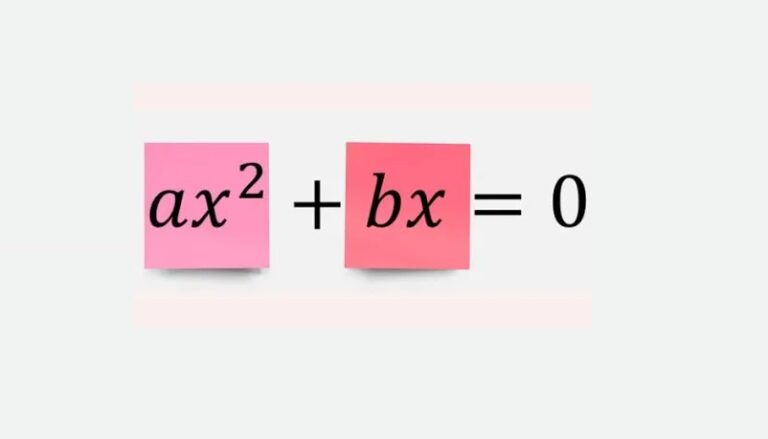
0 comentários