O fluxo ($$\Phi$$) representa o volume de sangue que atravessa uma sessão transversal de um vaso sanguíneo em um determinado intervalo de tempo. Esse fluxo pode ser calculado pela razão entre a diferença de pressão do sangue nas duas extremidades do vaso ($$P_{1}$$ e $$P_{2}$$), também chamada de gradiente de pressão, e a resistência vascular (R), que é a medida da dificuldade de escoamento do fluxo sanguíneo, decorrente, principalmente, da viscosidade do sangue ao longo do vaso. A figura ilustra o fenômeno descrito.
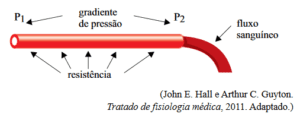
Assim, o fluxo sanguíneo $$\Phi$$ pode ser calculado pela seguinte fórmula, chamada de lei de Ohm:
\[\Phi = \frac{(P_{1} – P_{2})}{R}\]
Considerando a expressão dada, a unidade de medida da resistência vascular (R), no Sistema Internacional de Unidades, está corretamente indicada na alternativa
(A) $$\frac{kg\cdot s}{m^{5}}$$
(B) $$\frac{kg\cdot m^{4}}{s}$$
(C) $$\frac{kg\cdot s^{2}}{m}$$
(D) $$\frac{kg}{m^{4}\cdot s}$$
(E) $$\frac{kg^{2}\cdot m^{5}}{s^{2}}$$
Solução:
A resistência vascular pode ser escrita como $$R = \frac{P}{\Phi}$$. A unidade de $$P$$ é [$$\frac{N}{m^{2}}$$] e a unidade de $$\Phi$$ é [$$\frac{m^{3}}{s}$$]. Logo \[R = \frac{P}{\Phi} \longrightarrow R = \frac{Pa}{\frac{m^{3}}{s}} \longrightarrow R = \frac{\frac{N}{m^{2}}}{\frac{m^{3}}{s}} \longrightarrow R = \frac{\frac{kg\cdot\frac{m}{s^{2}}}{m^{2}}}{\frac{m^{3}}{s}} \longrightarrow R = \frac{kg}{m^{4}\cdot s}\] Resposta: letra D.


















Um comentário