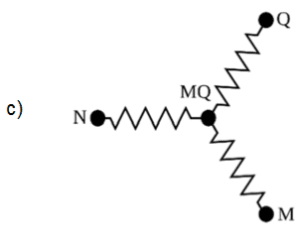
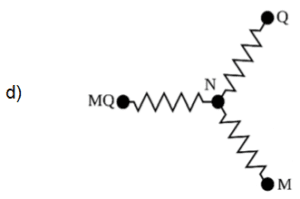
Muitos dispositivos de aquecimento usados em nosso cotidiano usam resistores elétricos como fonte de calor. Um exemplo é o chuveiro elétrico, em que é possível escolher entre diferentes opções de potência usadas no aquecimento da água, por exemplo, morno (M), quente (Q) e muito quente (MQ). Considere um chuveiro que usa a associação de três resistores, iguais entre si, para oferecer essas três opções de temperatura. A escolha é feita por uma chave que liga a rede elétrica entre o ponto indicado pela letra N e um outro ponto indicado por M, Q ou MQ, de acordo com a opção de temperatura desejada. O esquema que representa corretamente o circuito equivalente do chuveiro é
![]()
![]()
Confira nossa Lista de Exercícios Resolvidos de Circuitos Elétricos e Leis de Ohm
Solução:
A potência é o que deixa a água mais ou menos quente. Para calcular a potência do resistor podemos utilizar $$P = \frac{U^{2}}{R}$$. Assim vemos que quanto maior a resistência, menor a potência e menos quente fica a água. Portanto vemos que $$R_{NMQ}<R_{NQ}<R_{NM}$$. Consequentemente, a potência será $$P_{NMQ}>P_{NQ}>P_{NM}$$. Portanto os pontos N, Muito Quente (MQ), Quente (Q) e Morno (M), devem aparecer em série, nessa ordem.
Resposta: letra A.

















