Concurso Nacional Unificado – CNU
A Figura representa um círculo cujo centro é o ponto P.
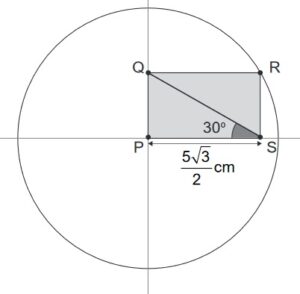
O retângulo PQRS é tal que o lado PS mede (5√3)/2 cm, o ponto R pertence à circunferência, e o ângulo PSQ mede 30º.O valor numérico da medida da área do círculo, em cm², é igual a…
Solução:
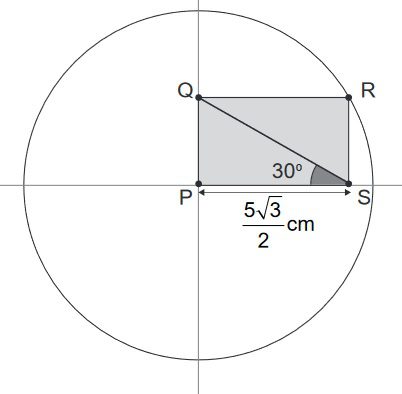
1) Utilizando o retângulo PQRS, observamos que a diagonal QS, medindo $$x$$, pode ser obtida pela relação trigonométrica do cosseno no triângulo QPS. De fato, a diagonal é a hipotenusa de QPS, e PS é o cateto adjacente ao ângulo de 30º, logo $$\frac{\sqrt{3}}{2}=cos(30º)=\frac{\frac{5\sqrt{3}}{2}}{x}$$.
Cancelando a fração $$\frac{\sqrt{3}}{2}$$ dos dois lados da equação, obtemos $$x= 5$$ cm.
Questões Resolvidas do Concurso Nacional Unificado
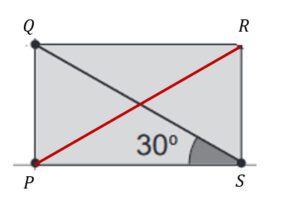
2) Embora a diagonal QS não represente o raio do círculo, sabemos que, em um retângulo, as diagonais têm o mesmo valor. Note que o segmento PR é a outra diagonal e coincide com o raio da circunferência em questão. Assim, como ambas as diagonais são iguais entre si e iguais ao raio, teremos $$r=5$$ cm.
3) A área do círculo é dada por $$\pi x^{2}$$, então teremos uma área de $$\pi\cdot 5^{2}=25\pi$$ cm².
0 comentários