A Equação de Clapeyron, também conhecida como Equação dos Gases Ideais, é uma relação fundamental na física e na química que descreve o comportamento dos gases. Essa equação combina as leis de Boyle, Charles e Gay-Lussac, estabelecendo uma conexão direta entre as principais variáveis que governam o estado de um gás.
Entendendo a Equação de Clapeyron
A fórmula clássica da equação é: $$PV=nRT$$.
Em que
- P é a pressão do gás (<atm, Pa, etc.>), 🔓
- V é o volume ocupado pelo gás (<L, m³, etc.>), 🌐
- n é a quantidade de matéria do gás (em mol) ,💸
- R é a constante dos gases ideais (<0,08206 L⋅atm/(mol⋅K) ou 8,314 J/(mol⋅K)>), ✨
- T é a temperatura absoluta em Kelvin (K), 🌡️
Como Aplicar a Equação de Clapeyron?
Essa equação permite prever e calcular o comportamento dos gases sob diversas condições. Veja algumas situações práticas:
- Cálculo de Pressão: Quer saber a pressão de um gás em um recipiente fechado? Essa equação vai te ajudar.
- Determinação de Volume: Descubra quanto espaço um gás ocupa em diferentes condições.
- Previsão de Mudanças de Estado: Avalie o impacto de variações na temperatura ou pressão sobre um gás.
Exemplo de Uso Prático
O gás natural proveniente da bacia petrolífera de Campos é constituído basicamente por gás metano ($$CH_{4}$$). Se o volume consumido por uma residência for de 30 m³ de $$CH_{4}$$(g), à temperatura de 27 °C e pressão de 1 atmosfera, a quantidade de mols consumida desse gás, em mol, será de:
Dados:
R = 0,082 atm · L · mol–1 · K–1;
Solução:
Primeiro preciso compatibilizar as unidades dos dados do exercício com a unidade da constante universal dos gases (R). A pressão já está em atm, precisamos transformar o volume de m³ para L e a temperatura de °C para K.
$$V = 30 m^{3}\cdot \frac{1000L}{1 m^{3}} \longrightarrow V = 30.000L = 3\cdot 10^{4} L$$
$$T = 27^{circ} C + 273 \longrightarrow T = 300K$$
Agora podemos utilizar a Equação de Clapeyron para descobrir a quantidade de mols de $$CH_{4}$$.
$$P\cdot V = n\cdot R\cdot T \longrightarrow 1\cdot 3\cdot 10^{4} = n\cdot 8,2\cdot 10^{-2}\cdot 3\cdot 10^{2} \longrightarrow$$
$$n = \frac{1\cdot 3\cdot 10^{4}}{8,2\cdot 10^{-2}\cdot 3\cdot 10^{2}} \longrightarrow n = 1,2 \cdot 10^{3}\, mol$$
Importância da Equação na Química e Engenharia 🔧✨
A Equação de Clapeyron é amplamente utilizada em diversas áreas, como:
- Indústria Química: Previsão do comportamento de gases em reatores.
- Engenharia Mecânica: Estudos sobre a eficiência de turbinas a gás.
- Física Atmosférica: Modelagem de fenômenos meteorológicos.
Dicas de Ouro 🔮
- Sempre converta a temperatura para Kelvin antes de aplicar a equação.
- Certifique-se de que todas as unidades sejam compatíveis.
- Use a constante dos gases ideais correta de acordo com as unidades escolhidas.
Curiosidades sobre Gases Ideais 🤔
Você sabia que gases reais nem sempre seguem perfeitamente essa equação? Em altas pressões e baixas temperaturas, desvios podem ocorrer, e modelos mais complexos, como a Equação de Van der Waals, são usados.
Conclusão
A Equação de Clapeyron é uma ferramenta poderosa para entender e prever o comportamento dos gases em diversas situações. Compreender essa relação é fundamental para estudantes e profissionais das ciências exatas e engenharias.
Gostou deste conteúdo? Compartilhe com seus amigos e deixe seu comentário! 🚀
















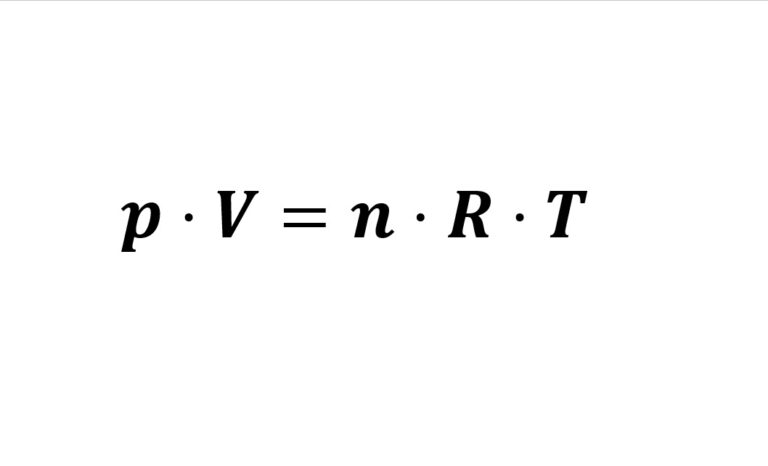
0 comentários