Progressão Aritmética: tudo sobre P.A, o que é, termo geral, soma, etc.

Progressão aritmética é uma sequência numérica em que a diferença entre qualquer termo e seu antecessor é igual à diferença entre o sucessor e aquele termo.

Exemplos

A sequência dos números naturais: 1,2,3,4… Note que 2-1 = 3-2 = 4-3 = 1, e assim por diante.

A sequência dos números ímpares: 1,3,5,7,…. Observe que 3-1 = 5-3 = 7-5 = 2, e assim por diante.

Isso significa que a diferença entre dois termos consecutivos é constante. Chamamos esse número de razão da progressão aritmética. Podemos ainda notar que qualquer termo é resultado da soma entre seu antecessor e a razão.

Exemplos

O segundo quarto da sequência de números pares é o terceiro somado à razão, isto é: $5 + 2 = 7$ .

O terceiro termo da sequência dos naturais é o segundo somado à razão: $3 + 1 = 4$ .

Termo Geral

Cada elemento de uma sequência é denotado por $a_{n}$ , em que $n$ representa o índice daquele termo.

Exemplos

Na sequência dos números ímpares, $a_{1} = 1, a_{2} = 3, a_{3} = 5$ ,…
Na sequência dos números pares, $a_{1} = 2, a_{2} = 4, a_{3} = 6$ ,…

Seja $r$ a razão de uma progressão aritmética. Sabemos que cada termo é o seu antecessor somado à razão, então podemos observar que

a₂=a₁+1r
a₃=a₂+r = a₁ + 2r
a₄ = a₃ + r = a₁ + 3r
a_n = a₁ + (n-1)r

Podemos concluir que qualquer temo de índice $n$ depende apenas do primeiro termo ( $a_{1}$ ) e da razão ( $r$ ), segundo a fórmula $a_{n} = a_{1} + (n - 1) \cdot r$ . Analogamente, podemos relacionar $a_{n}$ com outro termo genérico $a_{m}$ :

$a_{n} = a_{m} + (n - m) \cdot r .$

Essa fórmula é chamada de termo geral da progressão aritmética.

Exemplos

Sendo $r = 4$ e $a_{1} = 3$ , calcule o vigésimo termo.
$a_{20} = 3 + (20 - 1) \cdot 4 = 79$

Se $r = - 1$ e $a_{10} = 1$ , calcule o décimo quinto termo.
$a_{15} = a_{10} + (15 - 10) \cdot (- 1) = - 4$ .

Soma de uma Progressão Aritmética Finita

A soma dos $n$ primeiros termos de uma progressão aritmética é dada por

$S_{n} = n \frac{(a_{1} + a_{n})}{2} .$

Exemplos

Calcule a soma dos 100 primeiros números naturais. Como $a_{n} = n$ e $a_{1} = 1$ , teremos $S_{100} = 100 \frac{1 + 100}{2} = 5050$ .

Qual a soma dos 30 primeiros números pares?
Observe que $a_{1} = 2$ e $a_{n} = 2 n$ , então $S_{30} = 30 \cdot \frac{2 + 60}{2} = 930$ .

Propriedades da Progressão Aritmética

Uma propriedade útil mostra que qualquer termo é a média aritmética entre seu antecessor e seu sucessor. De fato, sabemos que qualquer elemento da progressão aritmética é resultado de seu antecessor somado à razão: $a_{n} = a_{n - 1} + r$ e $a_{n + 1} = a_{n} + r$ .

Daqui, obtemos $a_{n - 1} + a_{n + 1} = a_{n} - r + a_{n} + r = 2 a_{n}$ , logo

$a_{n} = \frac{a_{n - 1} + a_{n + 1}}{2} .$

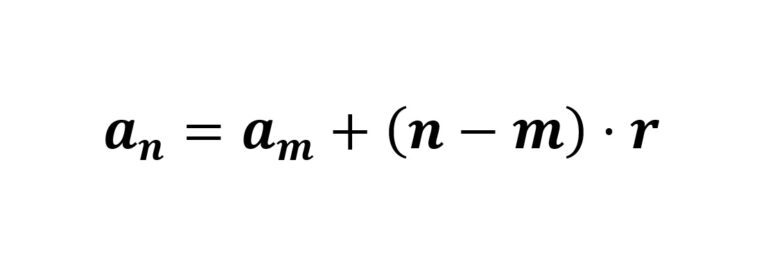
0 comentários