Questão
Em um dia de calmaria, um garoto sobre uma ponte deixa cair, verticalmente e a partir do repouso, uma bola no instante $$t_{0} = 0\, s$$. A bola atinge, no instante $$t_{4}$$, um ponto localizado no nível das águas do rio e à distância h do ponto de lançamento. A figura apresenta, fora de escala, cinco posições da bola, relativas aos instantes $$t_{0}$$, $$t_{1}$$, $$t_{2}$$, $$t_{3}$$ e $$t_{4}$$. Sabe-se que entre os instantes $$t_{2}$$ e $$t_{3}$$ a bola percorre 6,25 m e que $$g = 10 m/s^{2}$$.
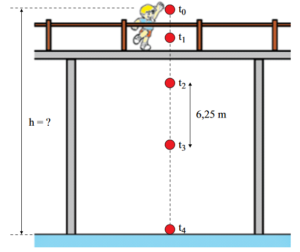
Desprezando a resistência do ar e sabendo que o intervalo de tempo entre duas posições consecutivas apresentadas na figura é sempre o mesmo, pode-se afirmar que a distância h, em metros, é igual a
(A) 25.
(B) 28.
(C) 22.
(D) 30.
(E) 20.
Solução:
Nós temos os tempos $$t_{0} = 0, t_{1} = t, t_{2} = 2t, t_{3} = 3t\,\, e\,\, t_{4} = 4t$$. A posição em função do tempo pode ser escrita como \[S = S_{0} + v_{0} t + \frac{at^{2}}{2} \longrightarrow S = 0 + 0\cdot t + \frac{10\cdot t^{2}}{2} \longrightarrow S = 5\cdot t^{2}\] Sabemos que $$S_{3} – S_{2} = 6,25\, m$$, então \[5\cdot t_{3} ^{2} – 5\cdot t_{2} ^{2} = 6,25 \longrightarrow 5\cdot (3t)^{2} – 5\cdot (2t)^{2} = 6,25 \longrightarrow t = \sqrt{0,25}\, s\] Agora podemos calcular $$S_{4} = h$$ \[S_{4} = h = 5\cdot (4t)^{2} \longrightarrow h = 5\cdot (4\cdot\sqrt{0,25})^{2} \longrightarrow h = 20\, m\] Resposta: letra E.
Questão
No dia 5 de junho de 2012, pôde-se observar, de determinadas regiões da Terra, o fenômeno celeste chamado trânsito de Vênus, cuja próxima ocorrência se dará em 2117.
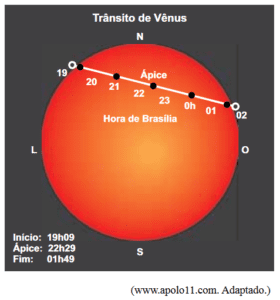
Tal fenômeno só é possível porque as órbitas de Vênus e da Terra, em torno do Sol, são aproximadamente coplanares, e porque o raio médio da órbita de Vênus é menor que o da Terra. Portanto, quando comparado com a Terra, Vênus tem
(A) o mesmo período de rotação em torno do Sol.
(B) menor período de rotação em torno do Sol.
(C) menor velocidade angular média na rotação em torno do Sol.
(D) menor velocidade escalar média na rotação em torno do Sol.
(E) menor frequência de rotação em torno do Sol.
Solução:
Sabemos que $$\frac{T^{2}}{R^{3}} = constante$$. Como o raio médio da órbita de Vênus é menor, o período de rotação de Vênus em torno do sol também deve ser menor para que a razão permaneça constante.
Resposta: letra B.
Questão
A figura ilustra um brinquedo oferecido por alguns parques, conhecido por tirolesa, no qual uma pessoa desce de determinada altura segurando-se em uma roldana apoiada numa corda tensionada. Em determinado ponto do percurso, a pessoa se solta e cai na água de um lago.
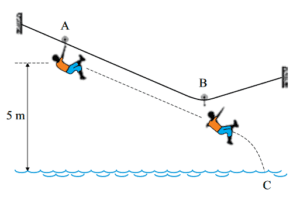
Considere que uma pessoa de 50 kg parta do repouso no ponto A e desça até o ponto B segurando-se na roldana, e que nesse trajeto tenha havido perda de 36% da energia mecânica do sistema, devido ao atrito entre a roldana e a corda. No ponto B ela se solta, atingindo o ponto C na superfície da água. Em seu movimento, o centro de massa da pessoa sofre o desnível vertical de 5 m mostrado na figura. Desprezando a resistência do ar e a massa da roldana, e adotando g = 10 m/s2, pode-se afirmar que a pessoa atinge o ponto C com uma velocidade, em m/s, de módulo igual a
(A) 8.
(B) 10.
(C) 6.
(D) 12.
(E) 4.
Solução:
Do ponto A ao ponto B perde-se 36% da energia. No ponto A temos $$E_{A} = m\cdot g\cdot h \longrightarrow E_{A} = 50\cdot 10\cdot 5 \longrightarrow E_{A} = 2500\, J$$. No ponto B temos $$E_{B} = 0,64\cdot E_{A} \longrightarrow E_{B} = 0,64\cdot 2500 \longrightarrow E_{B} = 1600\, J$$. A partir desse ponto não há mais perda de energia, logo do ponto B ao ponto C a energia se conserva: \[E_{B} = E_{C} \longrightarrow E_{B} = \frac{m\cdot v^{2}}{2} \longrightarrow 1600 = \frac{50\cdot v^{2}}{2} \longrightarrow v = 8\, m/s\] Resposta: letra A.
Questão
O relevo submarino de determinada região está representado pelas curvas de nível mostradas na figura, na qual os valores em metros representam as alturas verticais medidas em relação ao nível de referência mais profundo, mostrado pela linha vermelha.
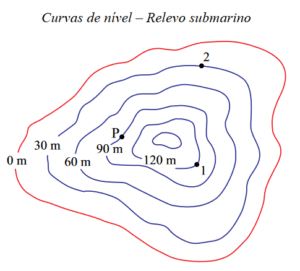
Dois peixes, 1 e 2, estão inicialmente em repouso nas posições indicadas e deslocam-se para o ponto P, onde param novamente. Considere que toda a região mostrada na figura esteja submersa, que a água do mar esteja em equilíbrio e que sua densidade seja igual a $$10^{3}\, kg/m^{3}$$. Se $$g = 10 m/s^{2}$$ e $$1\, atm = 10^{5}\, Pa$$, pode-se afirmar, considerando-se apenas os pontos de partida e de chegada, que, durante seu movimento, o peixe
(A) 2 sofreu uma redução de pressão de 3 atm.
(B) 1 sofreu um aumento de pressão de 4 atm.
(C) 1 sofreu um aumento de pressão de 6 atm.
(D) 2 sofreu uma redução de pressão de 6 atm.
(E) 1 sofreu uma redução de pressão de 3 atm.
Solução:
Precisamos calcular a variação de pressão dos pontos 1 e 2 pela equação $$P = d\cdot g\cdot h$$. Observe a figura:

Para o peixe 1: $$P_{1i} = 10^{3}\cdot 10\cdot 120 = 12\cdot 10^{5}\, Pa = 12\, atm$$ e $$P_{1f} = 10^{3}\cdot 10\cdot 90 = 9\cdot 10^{5}\, Pa = 9\, atm$$. Como o peixe 1 está descendo, temos um aumento de 3 atm na pressão.
Para o peixe 2: $$P_{2i} = 10^{3}\cdot 10\cdot 30 = 3\cdot 10^{5}\, Pa = 3\, atm$$ e $$P_{2f} = 10^{3}\cdot 10\cdot 90 = 9\cdot 10^{5}\, Pa = 9\, atm$$. Como o peixe 1 está subindo, temos uma redução de 6 atm na pressão.
Resposta: letra D.

















0 comentários