Para observar uma pequena folha em detalhes, um estudante utiliza uma lente esférica convergente funcionando como lupa. Mantendo a lente na posição vertical e parada a 3 cm da folha, ele vê uma imagem virtual ampliada 2,5 vezes.
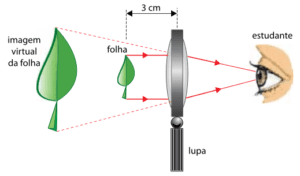
Considerando válidas as condições de nitidez de Gauss, a distância focal, em cm, da lente utilizada pelo estudante é igual a
(A) 5.
(B) 2.
(C) 6.
(D) 4.
(E) 3.
Confira nossa Lista de Exercícios Resolvidos de Espelhos e Lentes
Solução:
Sabemos que o tamanho da imagem ($$H_{i}$$) é 2,5 vezes o tamanho do objeto ($$H_{o}$$), ou seja, $$H_{i} = 2,5\cdot H_{o}$$. Podemos usar a proporção entre tamanhos e distâncias para encontrar a relação entre a distância do objeto à lente ($$D_{o}$$) e da imagem à lente ($$D_{i}$$) \[\frac{H_{i}}{H_{o}} = \frac{D_{i}}{D_{o}} \longrightarrow \frac{2,5\cdot H_{o}}{H_{o}} = \frac{D_{i}}{D_{o}} \longrightarrow D_{i} = 2,5\cdot D_{o} \longrightarrow D_{i} = 2,5\cdot 3 \longrightarrow D_{i} = 7,5\, cm\] Agora podemos encontrar o foco. Como a imagem é virtual, a distância dela à lente é negativa \[\frac{1}{f} = \frac{1}{D_{o}} + \frac{1}{D_{i}} \longrightarrow \frac{1}{f} = \frac{1}{3} – \frac{1}{7,5} \longrightarrow f = 5\, cm\] Resposta: letra A.

















0 comentários