Um objeto é disposto em frente a uma lente convergente, conforme a figura abaixo. Os focos principais da lente são indicados com a letra F. Pode-se afirmar que a imagem formada pela lente
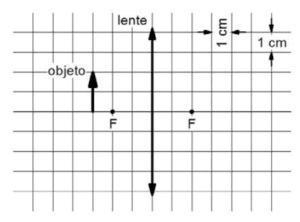
a) é real, invertida e mede 4 cm.
b) é virtual, direta e fica a 6 cm da lente.
c) é real, direta e mede 2 cm.
d) é real, invertida e fica a 3 cm da lente.
Confira nossa Lista de Exercícios Resolvidos de Espelhos e Lentes
Solução:
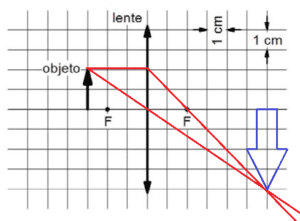
Utilizamos os raios especiais: entrando paralelo e saindo pelo foco, passando pelo vértice. Onde esses raios se cruzam, podemos desenhar a imagem. Vemos que ela é real, invertida e mede 4 cm.
Resposta: letra A.



