Questão
Em uma matriz, chamam-se elementos internos aqueles que não pertencem à primeira nem à última linha ou coluna. O número de elementos internos em uma matriz com 5 linhas e 6 colunas é igual a
a) 12.
b) 15.
c) 16.
d) 20.
Solução:
Há 30 elementos = $$6\cdot 5$$.
No total, as primeiras e últimas linhas e colunas possuem, juntas, $$2\cdot 5+2\cdot 6=10+12=22$$ elementos, com 4 repetidos, portanto há 18 elementos não internos ao todo.
Havendo 30 elementos da matriz, isso faz com que existam 30-18=12 elementos internos.
Resposta: a)
Questão
Considere o gráfico da função y=f(x) exibido na figura a seguir.

O gráfico da função inversa $$y=f^{-1}(x)$$ é dado por
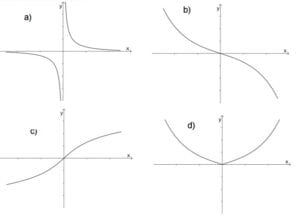
Solução:
Resposta: c)
Questão
A solução da equação na variável real $$x$$ , $$log_{x}(x+6)=2$$ , é um número
a) primo.
b) par.
c) negativo.
d) irracional.
Solução:
Aplique a definição de logaritmo, para obter a equação do segundo grau.
$$log_{x}(x+6)=2\Longleftrightarrow x^{2}=x+6\Longleftrightarrow x^{2}-x-6=0$$.
Resolvendo por Bhaskara, obtém-se:
\[x=\frac{1\pm \sqrt{1^{2}- 4\cdot(-6)}}{2}=\frac{1\pm\sqrt{25}}{2}\]. As raízes são $$\frac{1+5}{2}=3$$ e $$\frac{1-5}{2}=-2$$.
Mas a função logarítmica tem exige algumas condições de existência. $$log_{b}a$$ é a função logarítmica, se e somente se valem as seguintes condições:
- $$a>0$$
- $$b>0$$ e $$b\neq 1$$.
Da segunda condição, nota-se que a única base válida é $$x=3$$.
Resposta: a)

















