CEFET – MG | Lista de Exercícios

📝 André, Bruno, Cecília e Daniela disputam um jogo no qual, a cada rodada, são lançados um dado comum (numerado de 1 a 6) e uma moeda comum (cara e coroa nas faces).

Sabe-se que:

• André vencerá o jogo se obtiver, em três rodadas seguidas,
  coroa na face superior da moeda;
• Bruno vencerá o jogo se obtiver, em três rodadas seguidas,
  cara na face superior da moeda;
• Cecília vencerá o jogo se obtiver, em três rodadas seguidas,
  um número par na face superior do dado; e
• Daniela vencerá o jogo se obtiver, em três rodadas seguidas,
  três números iguais na face superior do dado.

Considere que já tenham sido realizadas duas rodadas. Na primeira rodada, foram obtidos cara na face superior da moeda e o número 2 na face superior do dado. Na segunda rodada, foram obtidos os mesmos resultados. Nessas condições, a chance de vitória no jogo na terceira rodada é maior para
A) André. | B) Bruno.
C) Cecília e Bruno. | D) Daniela e Cecília.
👉SOLUÇÃO

📝 Em uma escola, certa turma tem 44 estudantes. Desses estudantes, 29 gostam de Matemática e 32 gostam de Ciências, sendo que 22 gostam de Matemática e Ciências. Assim, a quantidade de estudantes dessa turma que não gostam de Matemática e nem de Ciências é igual a
A) 2 | B) 4 | C) 5 | D) 7
👉SOLUÇÃO

📝Sejam os conjuntos formados por elementos distintos tais que A = {x, 3, 4, 5, 6} e B = {y, 2, 4}, onde x e y ∈ N. Se A – B = {3, 5}, então a diferença x – y vale A) – 4 | B) – 2 | C) 2 | D) 4
👉SOLUÇÃO

📝Dentre os alunos de uma turma, considere M o conjunto daqueles que gostam de Matemática, G o conjunto dos que gostam de Geografia e P o conjunto dos alunos que gostam de Português. Assim, o conjunto dos alunos que não gostam de Geografia, mas gostam de Matemática ou de Português é, corretamente, representado por
A) G – (M ∪ P) | B) G – (M ∩ P)
C) (M ∩ P) – G | D) (M ∪ P) – G
👉SOLUÇÃO

📝Um motorista de táxi cobra, para cada corrida, uma taxa fixa de R$ 5,00 e mais R$ 2,00 por quilômetro rodado. O valor total arrecadado (R) num dia é função da quantidade total (x) de quilômetros percorridos e calculado por meio da função R(x) = ax + b, em que a é o preço cobrado por quilômetro e b a soma de todas as taxas fixas recebidas no dia. Se, em um dia, o taxista realizou 10 corridas e arrecadou R$ 410,00 então a média de quilômetros rodados por corrida, foi de:
A) 14 | B) 16 | C) 18 | D) 20
👉SOLUÇÃO

📝 Um site de compras lançou uma promoção em que uma lista de 8 produtos é oferecida com entrega grátis. Para ter direito à promoção, duas condições precisam ser satisfeitas:

1) Cada cliente não poderá comprar mais do que 1 unidade de um mesmo produto;
2) O valor mínimo da compra deverá ser de R$ 50,00. Na tabela, estão apresentados os produtos oferecidos nessa promoção e seus respectivos preços:

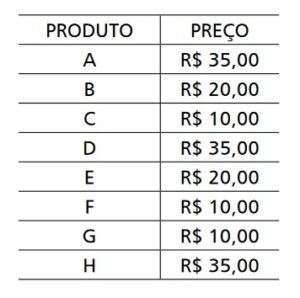Um cliente decidiu comprar o produto A, mas, para ter o benefício da entrega gratuita, adicionará produtos à compra a fim de gastar o mínimo possível. Dessa forma, de quantas maneiras diferentes esse cliente poderá fazer a escolha desses produtos?
A) 4 | B) 5 | C) 6 | D) 7
👉SOLUÇÃO 

📝 O sistema denominado ABO classifica os tipos sanguíneos em humanos de acordo com a presença, ou ausência, dos chamados antígenos A e B. Nesse sistema, caso o sangue possua os antígenos A e B, o sangue é considerado do tipo AB, caso possua apenas o antígeno A, é classificado como do tipo A, e caso possua apenas o antígeno B é classificado como o tipo B. Se o sangue não possuir nenhum desses antígenos, é considerado como tipo O.Considere um grupo de 100 pessoas, das quais 22 possuem o antígeno A e 19 possuem o antígeno B. Nessas condições, é correto afirmar que, dentre as pessoas desse grupo, a quantidade das que têm o tipo sanguíneo O é 

A) exatamente 59.
B) exatamente 78.
C) no mínimo 41 e no máximo 59.
D) no mínimo 59 e no máximo 78.
👉SOLUÇÃO 

📝Sejam as funções reais definidas por $$f(x) = (2/3)x – 1$$ e $$g(x) = x^{2}$$. Se $$h(x) = g(f(x))$$, afirma-se, corretamente, que h(x) é positiva para todo

A) x ∈ lR | B) x ∈ lR-{3/2}
C) x ∈ [-3/2 , 3/2] | D) x ∈ [-3/2,0] ∪ [3/2,0]
👉SOLUÇÃO