Um trem composto de uma locomotiva de comprimento L e de 19 vagões, todos também de comprimento L, está se deslocando, com aceleração constante, em um trecho da ferrovia. Um estudante, parado à margem da estrada e munido de equipamento adequado, mediu a velocidade do trem em dois instantes: $$V_{i} = 15\, m/s$$ quando passou por ele a extremidade dianteira do trem e, 20 segundos mais tarde, $$V_{f} = 25\, m/s$$, quando ele passou a extremidade traseira. Determine em metros, o comprimento L de cada vagão. Despreze o espaço entre os vagões.
Confira nossa lista de Exercícios de Função Horária da Velocidade no MUV
Confira nossa lista de Exercícios de Função Horária da Posição no MUV
Solução:
Primeiro temos que encontrar a aceleração do trem com a função horária da velocidade.
$$v_{f} = v_{0} + a*t \longrightarrow 25 = 15 + a*20 \longrightarrow a = 0,5\, m/s^{2}$$
Agora vamos utilizar a função horária da posição para encontrar a distância percorrida. Essa distância é o tamanho do trem todo.
$$S = S_{0} + v_{0} *t + \frac{a*t^{2}}{2} \longrightarrow S – S_{0} = 15*20 + \frac{0,5*20^{2}}{2} \longrightarrow \Delta S = 400\, m$$
O trem todo tem 400 m. São 19 vagões e uma locomotiva, todos medindo L. Então são 20 partes de tamanho L.
$$20L = 400 \longrightarrow L = 20\, m$$
















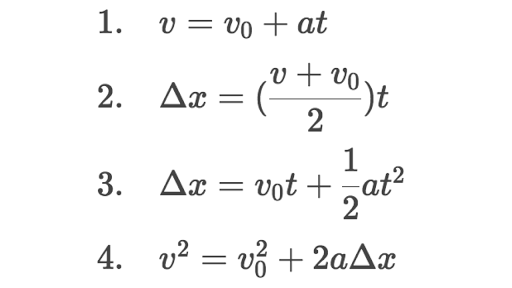
0 comentários