Em uma fábrica, há dois tanques, um no formato de um cilindro circular reto, com raio de base medindo R e altura medindo 2y, e outro no formato de um cone circular reto, com raio de base medindo 2R e altura medindo y, como indicado na Figura.
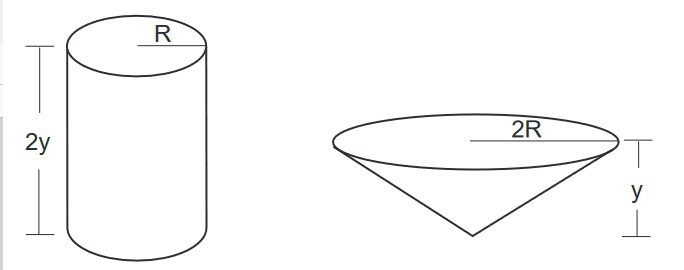
Considere que esses dois tanques estejam inicialmente vazios e despreze a espessura de suas superfícies. Sabe-se que uma torneira, de vazão constante, levou 2 h 24 min para encher completamente o tanque cilíndrico. O tempo necessário e suficiente para que essa mesma torneira, com a mesma vazão, encha completamente o tanque cônico é de
👉 Concurso Nacional Unificado – CNU
(A) 1 h 24 min
(B) 1 h 36 min
(C) 1 h 54 min
(D) 2 h 24 min
(E) 3 h 36 min
Solução:
1) O volume do cilindro é $$V_{cil}=\pi\cdot r^{2}\cdot h$$, em que $$h$$ é a altura do cilindro e $$r$$ é o raio da base. O volume do cone é $$V_{cone}=\pi\cdot r^{2}\frac{h}{3}$$, em que $$h$$ é a altura do cone e $$r$$ é o raio da base do cone.
No exercício, temos $$V_{cil}=2y\cdot\pi\cdot R^{2}$$ e $$V_{cone}=\frac{y\cdot \pi\cdot 4R^{2}}{3}$$.
2) Como uma hora tem 60 minutos, a que fração da hora correspondem os 24 minutos? Basta dividirmos por 60, e teremos $$24/60 = 0,4$$. O total de horas será de 2h + 0,4h = 2,4 horas.
3) A vazão despejada pela torneira é dada pela razão entre o volume e o tempo de enchimento. Observe que a vazão é constante (é igual) nos dois casos e que temos, pensando no cilindro, o resultado de $$\frac{2y\cdot\pi\cdot R^{2}}{2,4}$$. Igualando isso ao caso do cone, dado por $$\frac{V_{cone}}{t}$$, em que $$t$$ é o tempo necessário para que o cone fique completamente cheio, teremos
\[\frac{2y\cdot\pi\cdot R^{2}}{2,4}=\frac{\frac{y\cdot \pi\cdot 4R^{2}}{3}}{t}\Longrightarrow\]
\[\frac{2}{2,4}=\frac{4}{3t}\Longrightarrow\]
\[t = \frac{2\cdot 2,4}{3}=1,6 h.\]
4) 1,6 h equivale a 1 hora e 0,6 de uma hora. Para convertermos em minutos, basta multiplicarmos, então $$0,6\cdot 60 = 36$$ minutos. Como resultado, temos 1 hora e 36 minutos.
















0 comentários