O termo geral de uma progressão aritmética é a fórmula que nos permite calcular o valor de qualquer termo desta sequência, desde que tenhamos um elemento qualquer dela e sua razão. A apresentação mais usual do Termo Geral da P.A é
\[a_{n}=a_{1}+(n-1)\cdot r,\]
em que $$r$$ é a razão da progressão aritmética, $$n$$ é ordem do termo na sequência, $$a_{1}$$ é o termo de índice (ou ordem) 1 e $$a_{n}$$ é um termo de ordem (ou índice) $$n$$.
Exemplo
Numa progressão aritmética, a razão é 3 e o primeiro termo é -5. Qual o décimo termo (a10) ?
Os elementos do termo geral são $$a_{1}=-5$$ e $$r=3$$, então a fórmula será $$a_{n}=-5 + 3(n-1)$$.
Distribuindo, teremos $$a_{n}=3n – 8$$.
Para calcular o décimo termo, basta fazermos $$n=10$$, então $$a_{10}=3\cdot 10 – 8 = 22$$.
O Termo Geral pode ainda ser apresentado em função de outro elemento da sequência que não seja o termo inicial (a1). A fórmula é:
\[a_{n}=a_{m}+(n-m)\cdot r,\]
em que $$r$$ é a razão da progressão aritmética, $$n$$ é ordem do termo na sequência, $$a_{m}$$ é o termo de índice (ou ordem) m e $$a_{n}$$ é um termo de ordem (ou índice) $$n$$.
Exemplo
Numa progressão aritmética, a razão é 3 e o quinto termo é 7. Qual o décimo segundo termo (a12) ?
Os elementos do termo geral são $$a_{5}=7, r=3$$ e $$m=5$$, então a fórmula será $$a_{n}=7 + 3(n-5)$$. Distribuindo, teremos $$a_{n}=3n – 8$$.
O décimo segundo termo é $$a_{12}=3\cdot 12 – 8 = 28$$.
(Note que essa progressão é a mesma do primeiro exemplo!)
















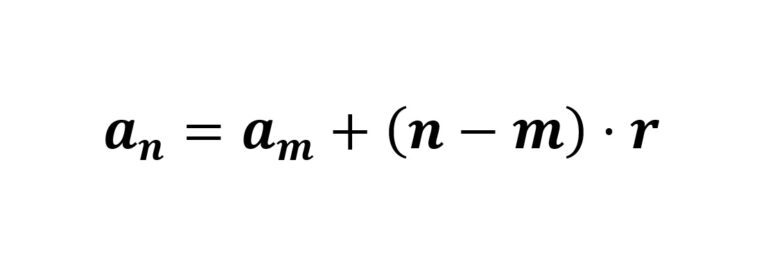
0 comentários