Duas ondas mecânicas transversais e idênticas, I e II, propagam-se em sentidos opostos por uma corda elástica tracionada. A figura 1 representa as deformações que a onda I, que se propaga para direita, provocaria em um trecho da corda nos instantes $$t = 0$$ e $$t = \frac{T}{4}$$, em que T é o período de oscilação das duas ondas. A figura 2 representa as deformações que a onda II, que se propaga para esquerda, provocaria no mesmo trecho da corda, nos mesmos instantes relacionados na figura 1. Ao se cruzarem, essas ondas produzem uma figura de interferência e, devido a esse fenômeno, estabelece-se uma onda estacionária na corda. A figura 3 representa a configuração da corda resultante da interferência dessas duas ondas, nos mesmos instantes $$t = 0$$ e $$t = \frac{T}{4}$$.
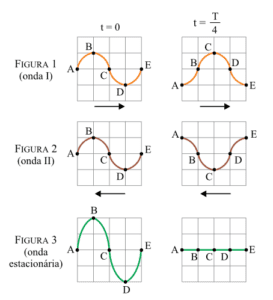
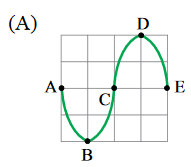
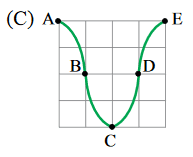
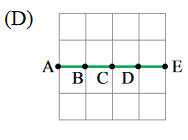
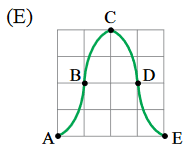
A figura que melhor representa a configuração da corda nesse mesmo trecho devido à formação da onda estacionária, no instante $$\frac{3T}{4}$$, está representada na alternativa

Confira nossa Lista de Exercícios Resolvidos de Harmônicos e Efeito Doppler
Solução:
Ao observarmos a figura, percebemos que a cada quarto de período cada ponto se move um quadradinho para cima ou para baixo. Portanto, daqui dois quartos de período, ou seja, em $$t = \frac{3T}{4}$$, o ponto C será um vale na primeira onda, enquanto o ponto C da segunda onda será uma crista. Logo, o resultado de sobreposição dessas duas ondas será igual a quando observamos o tempo $$t = \frac{T}{4}$$.
Resposta: letra D.

















0 comentários