Portal da Ondulatória: acesse aqui!
Lista de Ondulatória – Ondas, propriedades, equação da onda (clique aqui)
Estacionariedade e Harmônicos
Questão
(UNESP – 2014) Duas ondas mecânicas transversais e idênticas, I e II, propagam-se em sentidos opostos por uma corda elástica tracionada. A figura 1 representa as deformações que a onda I, que se propaga para direita, provocaria em um trecho da corda nos instantes $$t = 0$$ e $$t = \frac{T}{4}$$, em que T é o período de oscilação das duas ondas. A figura 2 representa as deformações que a onda II, que se propaga para esquerda, provocaria no mesmo trecho da corda, nos mesmos instantes relacionados na figura 1. Ao se cruzarem, essas ondas produzem uma figura de interferência e, devido a esse fenômeno, estabelece-se uma onda estacionária na corda. A figura 3 representa a configuração da corda resultante da interferência dessas duas ondas, nos mesmos instantes $$t = 0$$ e $$t = \frac{T}{4}$$.
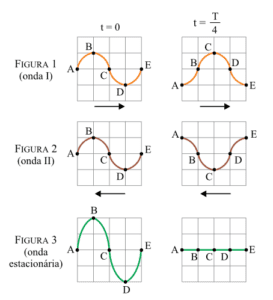
A figura que melhor representa a configuração da corda nesse mesmo trecho devido à formação da onda estacionária, no instante $$\frac{3T}{4}$$, está representada na alternativa
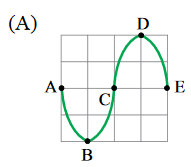

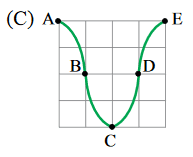
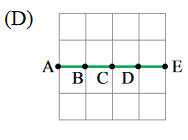
Questão
(UNICAMP – 2019) A levitação acústica consiste no emprego de ondas acústicas para exercer força sobre objetos e com isso mantê-los suspensos no ar, como a formiga representada na figura A, ou movimentá-los de forma controlada. Uma das técnicas utilizadas baseia-se na formação de ondas acústicas estacionárias entre duas placas, como ilustra a figura B, que mostra a amplitude da pressão em função da posição vertical.
a) As frequências de ressonância acústica entre duas placas, ou num tubo fechado nas duas extremidades, são dadas por $$f_{n} = \frac{nv}{2L}$$, sendo L a distância entre as placas, v = 340 m/s a velocidade do som no ar, e n um número inteiro positivo e não nulo que designa o modo. Qual é a frequência do modo ilustrado na figura B?
Questão
(FGV – 2018) As figuras 1 e 2 representam a mesma corda de um instrumento musical percutida pelo músico e vibrando em situação estacionária.
De uma figura para outra, não houve variação na tensão da corda. Assim, é correto afirmar que, da figura 1 para a figura 2, ocorreu
(A) um aumento na velocidade de propagação das ondas formadas na corda e também na velocidade de propagação do som emitido pelo instrumento.
(B) um aumento no período de vibração das ondas na corda, mas uma diminuição na velocidade de propagação do som emitido pelo instrumento.
(C) uma diminuição na frequência de vibração das ondas formadas na corda, sendo mantida a frequência de vibração do som emitido pelo instrumento.
(D) uma diminuição no período de vibração das ondas formadas na corda e também na velocidade de propagação do som emitido pelo instrumento.
(E) um aumento na frequência de vibração das ondas formadas na corda, sendo mantida a velocidade de propagação do som emitido pelo instrumento.
Questão
(UNESP – 2016/2)Um experimento foi feito com a finalidade de determinar a frequência de vibração de um diapasão. Um tubo cilíndrico aberto em suas duas extremidades foi parcialmente imerso em um recipiente com água e o diapasão vibrando foi colocado próximo ao topo desse tubo, conforme a figura 1. O comprimento L da coluna de ar dentro do tubo foi ajustado movendo-o verticalmente. Verificou-se que o menor valor de L, para o qual as ondas sonoras geradas pelo diapasão são reforçadas por ressonância dentro do tubo, foi de 10 cm, conforme a figura 2.
Considerando a velocidade de propagação do som no ar igual a 340 m/s, é correto afirmar que a frequência de vibração do diapasão, em Hz, é igual a
(A) 425.
(B) 850.
(C) 1360.
(D) 3400.
(E) 1700.
Questão
Um violonista pressiona com o dedo uma das cordas do violão para que, quando tocada, ela emita uma nota lá-padrão de frequência 440 Hz. Considerando que a velocidade do som é 340 m/s e que a corda está vibrando no modo fundamental, qual o comprimento do trecho da corda que está emitindo o som?
a) 77 cm
b) 38 cm
c) 30 cm
d) 20 cm
e) 16 cm
Questão
Um tubo sonoro, como o da figura acima, emite um som que se propaga no ar com velocidade de módulo 340 m/s. Pode-se afirmar que o comprimento de onda e a frequência da onda sonora emitida são, respectivamente:
a) 0,75 m e 340 Hz.
b) 0,80 m e 425 Hz.
c) 1,00 m e 230 Hz.
d) 1,50 m e 455 Hz.
e) 2,02 m e 230 Hz.
Questão
Têm-se dois tubos sonoros, A e B, cheios de ar. A é aberto e B, fechado, ambos com o comprimento de 85 cm. Quais as frequências fundamentais em Hz, em A e B, respectivamente, se a velocidade do som no ar é de 340 m/s?
a) 100 e 200
b) 100 e 400
c) 200 e 100
d) 300 e 400
e) 400 e 300
Efeito Doppler
Questão
(FUVEST – 2016) Miguel e João estão conversando, parados em uma esquina próxima a sua escola, quando escutam o toque da sirene que indica o início das aulas. Miguel continua parado na esquina, enquanto João corre em direção à escola. As ondas sonoras propagam-se, a partir da sirene, em todas as direções, com comprimento de onda λ = 17cm e velocidade $$V_{S} = 340\, m/s$$, em relação ao ar. João se aproxima da escola com velocidade de módulo $$v = 3,4\, m/s$$ e direção da reta que une sua posição à da sirene. Determine
a) a frequência $$f_{M}$$ do som da sirene percebido por Miguel parado na esquina;
b) a velocidade $$v_{R}$$ do som da sirene em relação a João correndo;
c) a frequência $$f_{J}$$ do som da sirene percebido por João quando está correndo.
Miguel, ainda parado, assobia para João, que continua correndo. Sendo o comprimento de onda do assobio igual a 10 cm, determine
d) a frequência $$f_{A}$$ do assobio percebido por João.
Note e adote: Considere um dia seco e sem vento.
Questão
(UEMG – 2018)Assinale a alternativa que apresenta fenômenos que poderiam estar associados às seguintes ilustrações.
(A) Ressonância magnética e oscilações forçadas.
(B) Efeito Casimir e Ultrassom.
(C) Efeito Doppler e Desvio para o Vermelho (Big Bang).
(D) Ressonância acústica e interferência destrutiva.
Questão
(ENEM – 2016) Uma ambulância A em movimento retílineo e uniforme aproxima-se de um observador O, em repouso. A sirene emite um som de frequência constante $$f_{A}$$. O desenho ilustra as frentes de onda do som emitido pela ambulância. O observador possui um detector que consegue registrar, no esboço de um gráfico, a frequência da onda sonora detectada em função do tempo $$f_{O}(t)$$, antes e depois da passagem da ambulância por ele.
Qual esboço gráfico representa a frequência $$f_{O}(t)$$ detectada pelo observador?


















0 comentários