Questão
A figura abaixo mostra a precipitação pluviométrica em milímetros por dia (mm/dia) durante o último verão em Campinas. Se a precipitação ultrapassar 30 mm/dia, há um determinado risco de alagamentos na região.
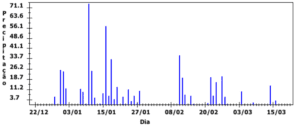
De acordo com o gráfico, quantos dias Campinas teve este risco de alagamento? (Fonte: http://www.agritempo.gov.br/agroclima/plotpesq. Acessado em 10/10/2012.)
a) 2 dias.
b) 4 dias.
c) 6 dias.
d) 10 dias.
Solução:
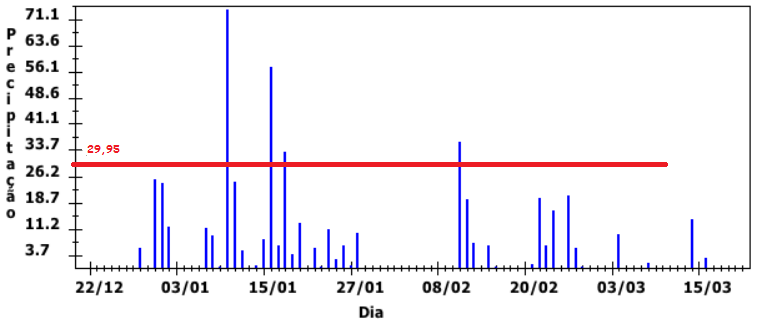
Observando que a diferença ,entre os números apresentados no eixo das ordenadas, é 7,5 mm/dia , traçamos a reta em destaque sobre a medida de 29,95 mm/dia. O número de barras azuis que superarem esta marca será o número de dias em que houve risco de alagamento.
Resposta: b)
Questão
Para repor o teor de sódio no corpo humano, o indivíduo deve ingerir aproximadamente 500 mg de sódio por dia. Considere que determinado refrigerante de 350 ml contém 35 mg de sódio. Ingerindo-se 1.500 ml desse refrigerante em um dia, qual é a porcentagem de sódio consumida em relação às necessidades diárias?
a) 45%.
b) 60%.
c) 30%.
d) 15%.
Solução:
A proporção entre o volume do refrigerante e a massa do sódio estabelecerá quanto se consome do sal, ao ingeri-se 1.500mL do produto.
350 mL ——— 35mg
1500 mL ——— $$x$$
$$350x=1500\cdot 35\longrightarrow x=\frac{1500\cdot 35}{350}=\frac{1500}{10}=150 mg_{sal}$$.
A porcentagem é $$\frac{150}{500}=\frac{15}{50}=\frac{3\cdot 5}{5\cdot 5\cdot 2}=0,3=30%$$.
Resposta: c)
Questão
Um automóvel foi anunciado com um financiamento “taxa zero” por R$ 24.000,00 (vinte e quatro mil reais), que poderiam ser pagos em doze parcelas iguais e sem entrada. Para efetivar a compra parcelada, no entanto, o consumidor precisaria pagar R$ 720,00 (setecentos e vinte reais) para cobrir despesas do cadastro. Dessa forma, em relação ao valor anunciado, o comprador pagará um acréscimo
a) inferior a 2,5%.
b) entre 2,5% e 3,5%.
c) entre 3,5% e 4,5%.
d) superior a 4,5%.
Solução:
Na prática, o comprador pagará um total de R$ 24.720,00 no valor do veículo, ao invés do valor de tabela anunciado. Por este motivo, o acréscimo dar-se-á sobre o valor de tabela (R$ 24.000,00).
\[V_{final}=V_{inicial}(1+i)=24720=24000(1+i)\Longrightarrow 1+i=\frac{24720}{24000}=1,03\Longrightarrow i = 0,03=3%\]
Resposta: b)


















0 comentários