No instante em que um veículo vai iniciar, à 72 km/h, a travessia de uma ponte de 80 m de altura, uma pessoa no interior do carro lança horizontalmente uma pedra, com velocidade de 5 m/s, perpendicular a sua velocidade em direção ao despenhadeiro. A pedra atinge o solo, no instante em que o veículo conclui a travessia. Calcule:
a) Qual o comprimento da ponte.
b) A posição da pedra, em relação ao veículo, quando ela atinge o solo.
Solução:
a) A pedra está em queda livre. Como o enunciado diz que a pedra chega no chão ao mesmo tempo que o carro chega no fim da ponte, basta calcular o tempo de queda da pedra e saberemos o tempo que demorou para o carro atravessar a ponte.
$$S_{f} = S_{0} + v_{0} t + \frac{at^{2}}{2} \longrightarrow 80 = 0 + 0 t + \frac{10t^{2}}{2} \longrightarrow t = 4\, s$$
Com esse tempo e a velocidade do carro, podemos encontrar o comprimento da ponte. A velocidade de 72 km/h corresponde a 20 m/s.
$$v = \frac{\Delta S}{\Delta t} \longrightarrow 20 = \frac{\Delta S}{4} \longrightarrow \Delta S = 80\, m$$
b) A pedra é lançada no começo da ponte, portanto sua posição em relação ao veículo é o seguimento $$\bar{BD}$$.
Primeiro precisamos do alcance da pedra, que corresponde ao seguimento $$\bar{AB}$$. Isso pode ser calculado com a velocidade horizontal da pedra e o tempo encontrado no item a).
$$v = \frac{\Delta S}{\Delta t} \longrightarrow 5 = \frac{\bar{AB}}{4} \longrightarrow \bar{AB} = 20\, m$$
Aplicando Pitágoras ao triângulo ABC, podemos calcular o segmento $$\bar{BC}$$.
$$\bar{BC}^{2} = \bar{AB}^{2} + \bar{AC}^{2} \longrightarrow \bar{BC}^{2} = 20^{2} + 80^{2} \longrightarrow \bar{BC} = \sqrt{400 + 6400} \longrightarrow \bar{BC} = \sqrt{6800}$$
Utilizando Pitágoras no triângulo BCD, podemos calcular o segmento $$\bar{BD}$$
$$\bar{BD}^{2} = \bar{BC}^{2} + \bar{CD}^{2} \longrightarrow \bar{BD}^{2} = (\sqrt{6800})^{2} + 80^{2} \longrightarrow \bar{BD} = \sqrt{6800 + 6400} \longrightarrow \bar{BD} = \sqrt{13200} \longrightarrow \bar{BD} = 114,9\, m$$
















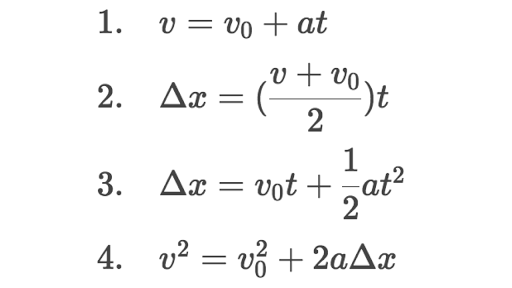
0 comentários