Construa uma aplicação linear $$T: P_2(\mathbb{R}) \longrightarrow M_2(\mathbb{R})$$ que satisfaça todas as condições abaixo:
- $$(1+x) \in Ker(T)$$.
- $$1 \notin Ker(T)$$.
- Existe um polinômio $$(r(x)\in P_2(\mathbb{R})$$ tal que \[T(r(x))=\begin{pmatrix}2 & 0\\-1 & 0\end{pmatrix}.\]
Resposta e passo a passo:
Uma possível resposta é $$T(p(x)) = T(a+bx+cx^{2}) = \begin{pmatrix}a-b & 0\\c & 0\end{pmatrix}.$$ No vídeo abaixo, eu mostro os detalhes de como eu obtive essa transformação linear.
















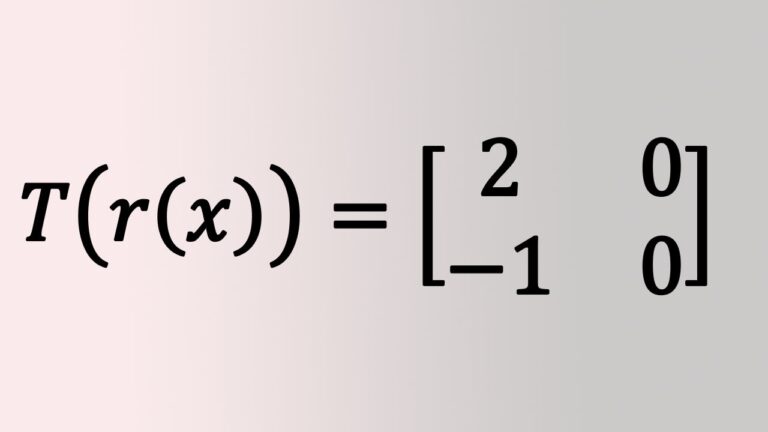
0 comentários