Questões sobre Vértice da Parábola

📝 Para uma determinada viagem, foi fretado um avião com 200 lugares. Cada pessoa deve pagar R$ 300,00 mais uma taxa de R$ 6,00 para cada lugar que ficar vago.

a)Qual a receita arrecadada se comparecerem 150 pessoas para a viagem?

b) Qual a máxima receita que pode ser arrecada nas condições do problema?

Respostas: a) R$ 90.000,00, b) R$ 93.750,00
Solução

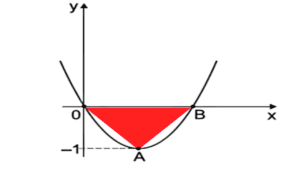
📝 Na figura, temos o gráfico de y = x² – 2px, de vértice A. A área do triângulo OAB é:

Solução

📝  A função f: R → R tem como gráfico uma parábola e satisfaz f(x + 1) – f(x) = 6x – 2, para todo número real x. Então, o menor valor de f(x) ocorre quando x é igual a:

a) 11/6 | b) 7/6 | c) 5/6 | d) 0 | e) – 5/6
Solução

📝Para abastecer seu estoque, um comerciante comprou um lote de camisetas ao custo de 16 reais a unidade. Sabe-se que em um mês, no qual vendeu (40 – x) unidades dessas camisetas ao preço unitário de x reais, o seu lucro foi máximo. Assim sendo, pela venda de tais camisetas nesse mês, o percentual de aumento repassado aos clientes, calculado sobre o preço unitário que o comerciante pagou na compra do lote, foi de

A) 80%. | B) 75%. | C) 60%. | D) 45%
Solução

📝 Considere a função polinomial ݂f : R → R definida por ax²+bx+c, em que a,b e c ∈ R e a ≠0. No plano cartesiano xy a única intersecção da reta y=2 com o gráfico de ݂ é o ponto (2,2) e a intersecção da reta x=0 com o gráfico de ݂f(x) é o ponto (0,-6).

O valor de a+b+c é
(A) –2 | (B) 0 | (C) 2 | (D) 4 | (E) 6

Gabarito: b)
Solução

📝O setor financeiro de uma indústria fabricante de produtos químicos notou que, com preços unitários de R$ 5,00 e R$ 6,00 por litro de determinado produto, as vendas mensais são, respectivamente, iguais a 2800 litros e 2000 litros. Com esses dados, o setor de análise quantitativa da indústria propôs modelar a relação entre o preço por litro x, em reais, e a quantidade f(x) de litros vendidos mensalmente por meio da função quadrática f(x) = 100x² + bx + c, sendo b e c constantes reais a serem determinadas. De acordo com esse modelo, o preço por litro desse produto que resulta no menor número de litros vendidos mensalmente é
(A) R$ 9,40. | (B) R$ 9,45. | (C) R$ 9,55.
(D) R$ 9,60. | (E) R$ 9,50.

Gabarito: e)
Solução

📝No plano cartesiano, o vértice da parábola de equação y = x(1-x) e os pontos em que ela intersecta o eixo das abscissas determinam um triângulo de área igual a

a) 3/16 | b) 1/5 | c) 1/16 | d) 1/4 | e) 1/8

Gabarito: e)
Solução