Exercícios Resolvidos de Razão e Proporção

Questão

(PUC – Campinas – 2014) Uma maquete de um reservatório cúbico foi construída em escala linear de 1:200. Se o volume da maquete do reservatório é de 64 cm3, a aresta do reservatório cúbico real, em metros, é igual a:

a) 4

b) 8

c) 16

d) 20

e) 32

Solução:

Sabendo que o volume do cubo é $$V=l^{3}$$, com $$l$$, o comprimento das arestas; temos como calcular o comprimento das arestas da maquete.

\[64=V=l^{3}\longrightarrow l=\sqrt[3]{64}=\sqrt[3]{2^{6}}=2^{6/3}=2^{2}=4cm\].

Utilizando a escala fornecida, calculamos o valor da aresta do objeto real.

1 u———- 200 cm (real)

4 cm (maquete) ———- x

$$x=4\cdot 200\longrightarrow x= 800cm= 8m$$ (real).

Resposta: b)

Questão

(PUC – Campinas – 2015) Considere a tabela abaixo da solubilidade do açúcar comum (sacarose) submetido a várias temperaturas

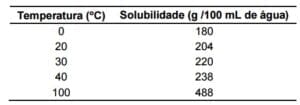
No preparo de uma calda com açúcar, uma receita utiliza 1 kg de açúcar para 0,5 litro de água. Nesse caso, a temperatura mínima necessária para que todo o açúcar se dissolva é

a) 0 °C.

b) 20 °C.

c) 30 °C.

d) 40 °C.

e) 100 °C.

Solução:

Para usar a tabela, é necessário calcular a solubilidade da receita em questão. Para isso, basta encontrar uma proporção semelhante àquelas apresentadas na tabela.

1 kg ————– 0,5 L equivale a

1000g ————– 500 mL

Se temos a proporção $$\frac{1000 g_{sacarose}}{500 ml_{água}}=\frac{200 g_{sacarose}}{100 ml_{água}}$$.

Na tabela, o mais próximo valor é para 204 g/mL. Portanto o valor mínimo para a temperatura é de 20 ºC.

Resposta: b)

Questão 

(UNICAMP – 2015) A tabela abaixo informa alguns valores nutricionais para a mesma quantidade de dois alimentos, A e B.

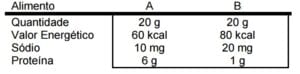
Considere duas porções isocalóricas (de mesmo valor energético) dos alimentos A e B. A razão entre a quantidade de proteína em A e a quantidade de proteína em B é igual a

a) 4.

b) 6.

c) 8.

d) 10.

Solução:

Resposta: c)

Questão 2

(PUC- Campinas – 2016-Meio do ano) A figura abaixo ilustra a regra de proporção utilizada pelos egípcios. Por essa regra, uma figura humana, em pé, deve ocupar 18 quadrados da sola do pé ao couro cabeludo. Nessa regra, ao ser desenhada uma figura humana, a linha 12 deve passar pela região lombar e a linha do joelho deve corresponder a 1/3 da altura da figura.

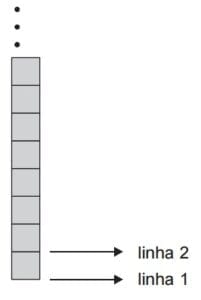
Supondo que fosse feito um desenho de figura humana sobre esse esquema de 18 quadrados, cada um com lado igual a 3,5 cm, a distância entre a linha da região lombar e a linha do joelho seria, em cm, de (A) 38,5.

(B) 12,5.

(C) 24,0.

(D) 17,5.

(E) 15,0.

[/kc_column_text][/kc_column][/kc_row]