Questão 18
A medida anunciada da tela de monitor retangular é a medida da sua diagonal, normalmente expressa em polegadas. A proporção entre a largura e a altura de uma dessas telas de 50 polegadas é 4 : 3. A área dessa tela, em unidade polegadas quadradas, é igual a
a) 1.250.
b) 1.600.
c) 1.200.
d) 1.440.
e) 960.
Solução:
Seja $$x$$ a largura e $$y$$, a altura.A área do retângulo é $$A=xy$$.
Da proporção apresentada, $$\frac{x}{y}=\frac{4}{3}\longrightarrow 3x=4y\longrightarrow y=(3/4)x$$. Substituindo este $$y$$ na equação anterior, tem-se $$A=x\cdot y=x\cdot(3x/4)=x^{2}(3/4)$$.
A informação acerca da diagonal permite-nos escrever, pelo teorema de Pitágoras.
$$x^{2}+y^{2}=50^{2}$$.
Substituindo o valor de $$x$$ anteriormente, temos
\[2500=50^{2}=x^{2}+y^{2}=x^{2}+(3x/4)^{2}=x^{2}(1+9/4)=x^{2}(25/16)\longrightarrow x^{2}=1600\]
Retomando na fórmula da área, $$A=x^{2}(3/4)=1600(3/4)=1200$$.
Resposta: c)
Questão 24
A figura abaixo ilustra a regra de proporção utilizada pelos egípcios. Por essa regra, uma figura humana, em pé, deve ocupar 18 quadrados da sola do pé ao couro cabeludo. Nessa regra, ao ser desenhada uma figura humana, a linha 12 deve passar pela região lombar e a linha do joelho deve corresponder a 1/3 da altura da figura.
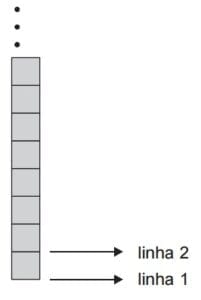
Supondo que fosse feito um desenho de figura humana sobre esse esquema de 18 quadrados, cada um com lado igual a 3,5 cm, a distância entre a linha da região lombar e a linha do joelho seria, em cm, de
a) 38,5.
b) 12,5.
c) 24,0.
d) 17,5.
e) 15,0.
Solução:
A altura do joelhos é de $$\frac{1}{3}\cdot 18\cdot 3,5=6\cdot 3,5$$ cm, isto é, resultado da multiplicação entre a altura dos quadrados com o número de quadrados e dividido por 3.
A lombar coincide com a coluna de número 12, portanto a altura da lombar será de 11 linhas abaixo da linha sobre a qual está, ou seja, $$11\cdot 3,5$$.
A diferença é $$11\cdot 3,5-6\cdot 3,5=5\cdot 3,5=17,5$$cm.
Resposta: d)
Questão 37
Questão 49
A figura abaixo é a reprodução de uma obra de Mondrian.
Junto a alguns lados dos retângulos estão marcadas referências às medidas de seus lados. A soma das áreas dos retângulos I e II corresponde, da área do retângulo III, aproximadamente, a
a) 78%.
b) 86%.
c) 81%.
d) 92%.
e) 74%.
Solução:
As áreas são calculadas como o produto entre a largura e a altura.
I – $$A_{I}=(b/2)a$$ ; II – $$A_{II}=ab$$ ; III – $$A_{III}=(7a/4)b$$.
$$A_{I}+A_{II}=ab/2 + ab = 3ab/2$$.
O percentual é calculado ao dividirmos a área menor pela área maior.
\[\frac{A_{I}+A_{II}}{A_{III}}=\frac{\frac{3ab}{2}}{\frac{7ab}{4}}=\frac{3ab}{2}\cdot\frac{4}{7ab}=\frac{12}{14}=\frac{6}{7}\cong 0,86=86%\]
Resposta: b)

















0 comentários