Questão
A figura abaixo exibe um quadrilátero ABCD, onde AB = AD e BC = CD = 2 cm. A área do quadrilátero ABCD é igual a
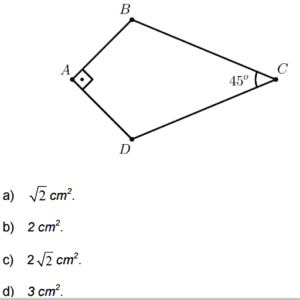
Solução:
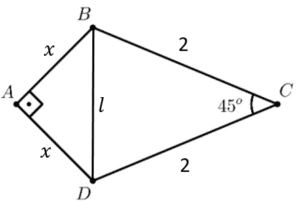
Usaremos a Lei dos Cossenos [$$a^{2}=b^{2}+c^{2} -2bc\cdot cos(\theta)$$] e a área dada pelo ângulo entre lados adjacentes de um triângulo [$$A=\frac{a\cdot b\cdot sen(\theta)}{2}$$].
No triângulo retângulo e isósceles, ABD, tem-se $$l^{2}=2x^{2}$$ e $$A=\frac{x^{2}}{2}=\frac{l^{2}}{4}$$.
No triângulo isósceles, BCD, tem-se, pela Lei dos Cossenos, $$l^{2}=4+4-8\frac{\sqrt{2}}{2}=8-4\sqrt{2}$$. Daqui, calcula-se a área de ABD: $$A=\frac{x^{2}}{2}=\frac{l^{2}}=\frac{8-4\sqrt{2}}{4}=2-\sqrt{2}$$.
A área de BCD é dada pela fórmula com o seno do ângulo, $$A=\frac{2\cdot 2\cdot\frac{\sqrt{2}}{2}}{2}=\sqrt{2}$$.
A soma das áreas dos triângulos resulta na área do quadrilátero: $$2-\sqrt{2}+\sqrt{2}=2cm^{2}$$.
Resposta: b)
Questão
Um cilindro circular reto, cuja altura é igual ao diâmetro da base, está inscrito numa esfera. A razão entre os volumes da esfera e do cilindro é igual a
Solução:
Questão
Considere o polinômio cúbico $$p(x)=x^{3}+x^{2}-ax-3$$, onde a é um número real. Sabendo que r e −r são raízes reais de p(x) , podemos afirmar que p(1) é igual a
a) 3.
b) 1.
c) -2.
d) -4.
Solução:
Usando a relação de Girard para a soma das raízes, temos $$r+(-r)+s=-\frac{b}{a}=-\frac{1}{1}=-1$$, deste modo $$s=-1$$, onde $$s$$ é a terceira raiz deste polinômio. Note que $$a$$ é o coeficiente de $$x^{3}$$, bem como $$b$$ é o coeficiente de $$x^{2}$$.
Como $$p(-1)=0$$, então $$(-1)^{3}+(-1)^{2}-a(-1)-3=0\Longrightarrow a-3=0\Longrightarrow a=3$$.
Além disso, sabe-se que $$p(1)=1^{3}+1^{2}-a-3=-a-1= -3-1=-4$$.
Resposta: d)
Questão
Considere o número complexo $$z=\frac{1+ai}{a-i}$$ , onde a é um número real e i é a unidade imaginária, isto é, $$i^{2}=-1$$. O valor de $$z^{2016}$$ é igual a
a) $$a^{2016}$$
b) 1.
c) 1 2016 + i .
d) i .
Solução:
Primeiro, elimine o denominador de $$z$$, multiplicando a fração pelo conjugado do denominador, isto é, o número $$a+i$$.
\[z=\frac{1+ai}{a-i}=\frac{1+ai}{a-i}\frac{a+i}{a+i}=\frac{(1+ai)(a+i}{(a+i)(a-i)}=\frac{a+i+ia^{2}+i^{2}a}{a^{2}-i^{2}}=i\frac{a+1}{a+1}=i\].
Agora, recorde que $$i^{3}=-i$$ , $$i^{4}=1$$ e que, para potências inteiras maiores que 5, o padrão repetir-se-á. Por isso, basta utilizar o Algoritmo da Divisão de Euclides, para obter 2016. De fato, $$2016=504\cdot 4$$, deste modo.
\[z^{2016}=i^{2016}=i^{504\cdot 4}=(i^{4})^{504}=1^{504}=1\]
Resposta: b)
Questão
A teoria da perspectiva, iniciada com o arquiteto Filippo Bruneleschi (1377-1446), utilizou conhecimentos geométricos e matemáticos na representação artística produzida na época. A figura a seguir ilustra o estudo da perspectiva em uma obra desse arquiteto. É correto afirmar que, a partir do Renascimento, a teoria da perspectiva
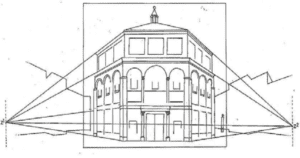
a) foi aplicada nas artes e na arquitetura, com o uso de proporções harmônicas, o que privilegiou o domínio técnico e restringiu a capacidade criativa dos artistas.
b) evidencia, em sua aplicação nas artes e na arquitetura, que as regras geométricas e de proporcionalidade auxiliam a percepção tridimensional e podem ser ensinadas, aprendidas e difundidas.
c) fez com que a matemática fosse considerada uma arte em que apenas pessoas excepcionais poderiam usar geometria e proporções em seus ofícios.
d) separou arte e ciência, tornando a matemática uma ferramenta apenas instrumental, porque essa teoria não reconhece as proporções humanas como base de medida universal.
Solução:
Resposta: b)

















0 comentários