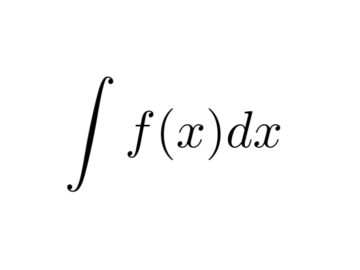Lista de exercícios resolvidos sobre integração do produto de potências de seno, cosseno, tangente, secante, cotangente e cossecante. $$\int cos^{2}(x)dx$$. Solução. $$\int cos^{3}(x)dx$$. Solução. $$\int...
Resolvendo a integral ∫tg²(x)sec³(x)dx.
Mostre, por meio de cálculos, que $$\int \frac{1}{x^{2}\sqrt{1+x^{2}}}dx=-\frac{\sqrt{1+x^{2}}}{x}$$. Solução:
Veja o passo a passo do cálculo da integral indefinida de cosseno ao cubo de x. $$\int cos^{3}(x)dx = sen(x)+\frac{sen^{3}(x)}{3}+k$$. Solução:
Vamos calcular $$\int cos(2x)dx$$. Solução: Fazendo $$u=2x$$, temos $$du = 2 dx$$. Pelo Teorema da Substituição, nossa integral passa a ser igual a \[(1/2)\int cos(u)...
Como mostrar que ∫cos²(x) dx = (1/4)[sen(2x)+2x] + k ? Veja a resolução aqui:
Uma lista de exercícios de integrais resolvidos e comentados! Integrais imediatas, integral por substituição, integração por partes, frações parciais, áreas de figuras e aplicações das...
Como calcular a integral indefinida (primitiva) do logaritmo natural de x? Veja a resolução neste artigo, com detalhamento e passo a passo. Solução: Vamos calcular...
Calcule $$\int\frac{1}{v^{2}+1}dv$$. Solução:
Calcule $$\int sen^{3}(x)cos^{2}(x)dx$$. Solução:
Exercício Uma partícula de massa m desloca-se sobre uma reta real sob ação do campo de forças f , onde f é uma função contínua...
Acheguem-se, amigos, à nossa página e estudemos o tópico deste post: Integral por Partes. A primeira coisa é recordar-se da fórmula da derivada do produto...
