A figura representa, de forma simplificada, o autódromo de Tarumã, localizado na cidade de Viamão, na Grande Porto Alegre. Em um evento comemorativo, três veículos de diferentes categorias do automobilismo, um kart (K), um fórmula 1 (F) e um stock-car (S), passam por diferentes curvas do circuito, com velocidades escalares iguais e constantes.
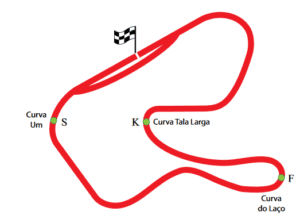
As tabelas 1 e 2 indicam, respectivamente e de forma comparativa, as massas de cada veículo e os raios de curvatura das curvas representadas na figura, nas posições onde se encontram os veículos.

Sendo $$F_{K}$$, $$F_{F}$$ e $$F_{S}$$ os módulos das forças resultantes centrípetas que atuam em cada um dos veículos nas posições em que eles se encontram na figura, é correto afirmar que
(A) $$F_{S} < F_{F} < F_{K}$$.
(B) $$F_{S} < F_{K} < F_{F}$$.
(C) $$F_{F} < F_{S} < F_{K}$$.
(D) $$F_{K} < F_{F} < F_{S}$$.
(E) $$F_{K} < F_{S} < F_{F}$$.
Confira nossa lista de Exercícios de Força Centrípeta
Solução:
Vamos calcular a força centrípeta para cada carro de acordo com a equação: $$F_{c} = m\cdot\frac{v^{2}}{R}$$.
Kart: $$F_{K} = M\cdot\frac{v^{2}}{2\cdot R} \longrightarrow F_{K} = \frac{1}{2}\cdot \frac{M\cdot v^{2}}{R}$$.
Fórmula 1: $$F_{F} = 3\cdot M\cdot\frac{v^{2}}{R} \longrightarrow F_{K} = 3\cdot \frac{M\cdot v^{2}}{R}$$
Stock-car: $$F_{S} = 6\cdot M\cdot\frac{v^{2}}{3\cdot R} \longrightarrow F_{K} = 2\cdot \frac{M\cdot v^{2}}{R}$$.
Podemos dizer que $$F_{K}<F_{S}<F_{F}$$.
Resposta: letra E.
















0 comentários