Em um jogo de sinuca, a bola A é lançada com velocidade $$\vec{V}$$ de módulo constante e igual a 2 m/s em uma direção paralela às tabelas (laterais) maiores da mesa, conforme representado na figura 1. Ela choca-se de forma perfeitamente elástica com a bola B, inicialmente em repouso, e, após a colisão, elas se movem em direções distintas, conforme a figura 2.
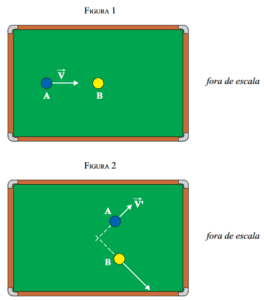
Sabe-se que as duas bolas são de mesmo material e idênticas em massa e volume. A bola A tem, imediatamente depois da colisão, velocidade $$\vec{V’}$$ de módulo igual a 1 m/s. Desprezando os atritos e sendo $$Eꞌ_{B}$$ a energia cinética da bola B imediatamente depois da colisão e $$E_{A}$$ a energia cinética da bola A antes da colisão, a razão $$\frac{E’_{B}}{E_{A}}$$ é igual a
(A) $$\frac{3}{4}$$
(B) $$\frac{1}{2}$$
(C) $$\frac{4}{5}$$
(D) $$\frac{2}{3}$$
(E) $$\frac{1}{5}$$
Confira nossa Lista de Exercícios Resolvidos de Energia
Solução:
Como a colisão é perfeitamente elástica, podemos considerar que a energia cinética se conserva. \[E_{A} = E’_{A} + E’_{B} \longrightarrow \frac{m\cdot 2^{2}}{2} = \frac{m\cdot 1^{2}}{2} + E’_{B} \longrightarrow E’_{B} = \frac{3\cdot m}{2}\] Como $$E_{A} = \frac{m\cdot 2^{2}}{2}$$, podemos escrever \[\frac{E’_{B}}{E_{A}} = \frac{\frac{3\cdot m}{2}}{\frac{m\cdot 2^{2}}{2}} \longrightarrow \frac{E’_{B}}{E_{A}} = \frac{1}{5}\]
Resposta: letra E.

















0 comentários