Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54 km/h (15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h. O gráfico representa como variou a velocidade escalar do veículo em função do tempo, enquanto ele passou por esse trecho da rodovia.
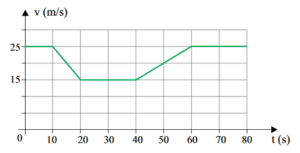
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria percorrido nessa estrada seria, em metros, de
(A) 1 650.
(B) 800.
(C) 950.
(D) 1 250.
(E) 350.
Confira nossa Lista de Exercícios Resolvidos de MUV
Solução:
A distância percorrida pelo carro é a área abaixo do gráfico. Se o carro não tivesse reduzido a velocidade, a área seria um retângulo de (25 m/s x 80 s). Porém, com a redução, precisamos descontar a área do trapézio. Essa é a distância adicional que o carro teria andado. Portanto \[\Delta S = \frac{(B + b)\cdot h}{2} \longrightarrow \Delta S = \frac{(50\, s + 20\, s)\cdot 10\, m/s}{2} \longrightarrow \Delta S = 350\, m\] Resposta: letra E.

















0 comentários