Portal da Cinemática: acesse aqui!
Nesta lista, encontram-se exercícios de Física, da área de Mecânica – Cinemática. Com os tópicos: deslocamento, velocidade, movimento uniformemente variado, aceleração e relacionados.
1) (UNICAMP – 2016) A demanda por trens de alta velocidade tem crescido em todo o mundo. Uma preocupação importante no projeto desses trens é o conforto dos passageiros durante a aceleração. Sendo assim, considere que, em uma viagem de trem de alta velocidade, a aceleração experimentada pelos passageiros foi limitada a $$a_{max} = 0,09\cdot g$$, onde $$g = 10 m/s^{2}$$ é a aceleração da gravidade. Se o trem acelera a partir do repouso com aceleração constante igual a $$a_{max}$$, a distância mínima percorrida pelo trem para atingir uma velocidade de 1080 km/h corresponde a
a) 10 km.
b) 20 km.
c) 50 km.
d) 100 km.
2) (UNICAMP – 2015) Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com dimensões comparáveis às da Terra, composta predominantemente de diamante. Por ser muito frio, o astro, possivelmente uma estrela anã branca, teria tido o carbono de sua composição cristalizado em forma de um diamante praticamente do tamanho da Terra.
Considerando que a massa e as dimensões dessa estrela são comparáveis às da Terra, espera-se que a aceleração da gravidade que atua em corpos próximos à superfície de ambos os astros seja constante e de valor não muito diferente. Suponha que um corpo abandonado, a partir do repouso, de uma altura h = 54 m da superfície da estrela, apresente um tempo de queda t = 3,0 s. Desta forma, pode-se afirmar que a aceleração da gravidade na estrela é de
a) 8,0 m/s².
b) 10 m/s².
c) 12 m/s².
d) 18 m/s².
3) (FEI – 2016/2) Um carro passa por um posto policial com velocidade de 108 km/h e mantém esta velocidade constante. No mesmo instante um policial inicia uma perseguição ao carro, acelerando sua moto a uma taxa constante de 2 m/s². Qual é a distância percorrida pelo policial até alcançar o carro?
a) 500 m
b) 700 m
c) 750 m
d) 900 m
e) 1 000 m
4) (UNESP – 2011) No gráfico a seguir são apresentados os valores da velocidade V, em m/s, alcançada por um dos pilotos em uma corrida em um circuito horizontal e fechado, nos primeiros 14 segundos do seu movimento. Sabe-se que de 8 a 10 segundos a trajetória era retilínea. Considere g = 10 m/s² e que para completar uma volta o piloto deve percorrer uma distância igual a 400 m.
A partir da análise do gráfico, são feitas as afirmações:
I. O piloto completou uma volta nos primeiros 8 segundos de movimento.
II. O piloto demorou 9 segundos para completar uma volta.
III. A força resultante que agiu sobre o piloto, entre os instantes 8 e 10 segundos, tem módulo igual a zero.
IV. Entre os instantes 10 e 12 segundos, agiu sobre o piloto uma força resultante, cuja componente na direção do movimento é equivalente a três vezes o seu peso.
São verdadeiras apenas as afirmações
(A) I e III.
(B) II e IV.
(C) III e IV.
(D) I, III e IV.
(E) II, III e IV.
5) (UNESP – 2018/2) Um foguete lançador de satélites, partindo do repouso, atinge a velocidade de 5 400 km/h após 50 segundos. Supondo que esse foguete se desloque em trajetória retilínea, sua aceleração escalar média é de
a) 30 m/s².
b) 150 m/s².
c) 388 m/s².
d) 108 m/s².
e) 54 m/s².
6) (UNESP – 2014) Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54 km/h (15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h. O gráfico representa como variou a velocidade escalar do veículo em função do tempo, enquanto ele passou por esse trecho da rodovia.
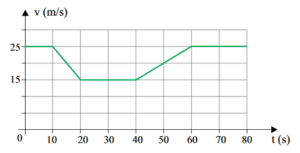
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria percorrido nessa estrada seria, em metros, de
a) 1 650.
b) 800.
c) 950.
d) 1 250.
e) 350.
7) (UERJ – 2018) Um carro se desloca ao longo de uma reta. Sua velocidade varia de acordo com o tempo, conforme indicado no gráfico.
A função que indica o deslocamento do carro em relação ao tempo t é:
(A) $$5t-0,55t^{2}$$
(B) $$5t+0,625t^{2}$$
(C) $$20t-1,25t^{2}$$
(D) $$20t+2,5t^{2}$$
8) (ENEM – 2017) Um motorista que atende a uma chamada de celular é levado à desatenção, aumentando a possibilidade de acidentes ocorrerem em razão do aumento de seu tempo de reação. Considere dois motoristas, o primeiro atento e o segundo utilizando o celular enquanto dirige. Eles aceleram seus carros inicialmente a 1,00 m/s². Em resposta a uma emergência, freiam com uma desaceleração igual a 5,00 m/s².
O motorista atento aciona o freio à velocidade de 14,0 m/s, enquanto o desatento, em situação análoga, leva 1,00 segundo a mais para iniciar a frenagem.
Que distância o motorista desatento percorre a mais do que o motorista atento, até a parada total dos carros?
A) 2,90 m.
B) 14,0 m.
C) 14,5 m.
D) 15,0 m.
E) 17,4 m.
9) (UNESP – 2017/2) No período de estiagem, uma pequena pedra foi abandonada, a partir do repouso, do alto de uma ponte sobre uma represa e verificou-se que demorou 2,0 s para atingir a superfície da água. Após um período de chuvas, outra pedra idêntica foi abandonada do mesmo local, também a partir do repouso e, desta vez, a pedra demorou 1,6 s para atingir a superfície da água.
Considerando a aceleração gravitacional igual a 10 m/s² e desprezando a existência de correntes de ar e a sua resistência, é correto afirmar que, entre as duas medidas, o nível da água da represa elevou-se
(A) 5,4 m.
(B) 7,2 m.
(C) 1,2 m.
(D) 0,8 m.
(E) 4,6 m.
10) (UNICAMP – 2008 – adaptada) Uma possível solução para a crise do tráfego aéreo no Brasil envolve o emprego de um sistema de trens de alta velocidade conectando grandes cidades. Há um projeto de uma ferrovia de 400km de extensão que interligará as cidades de São Paulo e Rio de Janeiro por trens que podem atingir até 300km/h. Considere um trem viajando em linha reta com velocidade constante. A uma distância de 30km do final do percurso, o trem inicia uma desaceleração uniforme de 0,06m/s², para chegar com velocidade nula a seu destino. Calcule a velocidade do trem no início da desaceleração.
11) (UNICAMP – 2006) Um corredor de 100 metros rasos percorre os 20 primeiros metros da corrida em 4,0 s com aceleração constante. A velocidade atingida dos 4,0 s é, então, mantida constante até o final da corrida.
a) Qual é a aceleração do corredor nos primeiros 20 m da corrida ?
b) Qual é a velocidade atingida ao final dos primeiros 20 m ?
c) Qual é o tempo gasto pelo corredor em toda a prova ?
12) (UNICAMP – 2018) Nos cruzamentos de avenidas das grandes cidades é comum encontrarmos, além dos semáforos tradicionais de controle de tráfego de carros, semáforos de fluxo de pedestres, com cronômetros digitais que marcam o tempo para a travessia na faixa de pedestres.
a) No instante em que o semáforo de pedestres se torna verde e o cronômetro inicia a contagem regressiva, uma pessoa encontra-se a uma distância $$d = 20 m$$ do ponto de início da faixa de pedestres, caminhando a uma velocidade inicial $$v_{0} = 0,5 m/s$$ . Sabendo que ela inicia a travessia da avenida com velocidade $$v = 1,5 m/s$$ , calcule a sua aceleração constante no seu deslocamento em linha reta até o início da faixa.
b) Considere agora uma pessoa que atravessa a avenida na faixa de pedestres, partindo de um lado da avenida com velocidade inicial $$v_{0} = 0,4 m/s$$ e chegando ao outro lado com velocidade final $$v = 1,2 m/s$$. O pedestre realiza todo o percurso com aceleração constante em um intervalo de tempo de $$t = 15 s$$ . Construa o gráfico da velocidade do pedestre em função do tempo e, a partir do gráfico, calcule a largura da avenida.
13) Quando um motorista aumenta a velocidade escalar de seu automóvel de 60 km/h para 78 km/h em 10 s, ele está comunicando ao carro uma aceleração escalar média, em m/s², de:
a) 18
b) 0,2
d) 1,8
c) 5,0
e) 0,5
14) Você foi contratado para sincronizar os quatro semáforos de uma avenida, indicados pelas letras O, A, B e C, conforme a figura.
Os semáforos estão separados por uma distância de 500 m. Segundo os dados estatísticos da companhia controladora de trânsito, um veículo, que está inicialmente parado no semáforo O, tipicamente parte com aceleração constante de $$1\, m s^{-2}$$ até atingir a velocidade de $$72\, km h^{-1}$$ e, a partir daí, prossegue com velocidade constante. Você deve ajustar os semáforos A, B e C de modo que eles mudem para a cor verde quando o veículo estiver a 100 m de cruzá-los, para que ele não tenha que reduzir a velocidade em nenhum momento. Considerando essas condições, aproximadamente quanto tempo depois da abertura do semáforo O os semáforos A, B e C devem abrir, respectivamente?
A) 20 s, 45 s e 70 s.
B) 25 s, 50 s e 75 s.
C) 28 s, 42 s e 53 s.
D) 30 s, 55 s e 80 s.
E) 35 s, 60 s e 85 s.
15) Os acidentes de trânsito são causados geralmente por excesso de velocidade. Em zonas urbanas no Brasil, o limite de velocidade normalmente adotado é de 60 km h−1. Uma alternativa para diminuir o número de acidentes seria reduzir esse limite de velocidade. Considere uma pista seca em bom estado, onde um carro é capaz de frear com uma desaceleração constante de 5 m s−2 e que o limite de velocidade reduza de 60 km h−1 para 50 km h−1. Nessas condições, a distância necessária para a frenagem desde a velocidade limite até a parada completa do veículo será reduzida em um valor mais próximo de
A) 1 m.
B) 9 m.
C) 15 m.
D) 19 m.
E) 38 m.
16) (UNESP – 2022) Quando a luz de um semáforo fica verde, um veículo parado parte com aceleração escalar constante, $$a_{1}$$, e se move por uma rua retilínea até atingir uma velocidade máxima, $$V_{m\acute{a} x}$$, em um intervalo de tempo $$T_{1}$$. A partir desse instante, inicia um processo de frenagem, também com aceleração escalar constante, até parar novamente, no semáforo seguinte, em um intervalo de tempo $$T_2$$. O gráfico representa a variação da velocidade desse veículo em função do tempo, nesse movimento.
No trajeto entre os dois semáforos, a velocidade escalar média desse veículo foi de:
(A) $$2\times a_{1}\times T_{1}$$
(B) $$\frac{a_1\times (T_{1} + T_{2})}{2}$$
(C) $$2\times a_{1}\times (T_{1} + T_{2})$$
(D) $$\frac{a_{1}\times T_{1}{2}$$
(E) $$a_{1}\times T_{1}$$
17) (UNESP – 2022) Dois amigos reuniram-se para empurrar um veículo de massa M, em linha reta, a partir do repouso, sobre uma superfície plana e horizontal. Entre as posições inicial e final, atuou sobre o veículo uma força resultante ($$F_{R}$$) que variou em função do tempo, em dois intervalos $$T_{1}$$ e $$T_{2}$$, conforme o gráfico.
No final do intervalo de tempo $$T_{1} + T_{2}$$, a velocidade escalar adquirida pelo veículo foi de:
(A) $$\frac{F(T_{1} + T_{2})}{M}$$
(B) $$\frac{F(T_{1} + 2T_{2})}{M}$$
(C) $$\frac{F(T_{1} + T_{2})}{2M}$$
(D) $$\frac{F(2T_{1} + T_{2})}{M}$$
(E) $$\frac{F(3T_{1} + T_{2})}{2M}$$
18) Um trem de 160 metros de comprimento está parado, com a frente da locomotiva posicionada exatamente no início de uma ponte de 200 metros de comprimento, num trecho de estrada retilíneo.Num determinado instante, o trem começa a atravessar a ponte com aceleração de 0,8m/s², que se mantém constante até que ele atravesse completamente a ponte.
a) Qual é a velocidade no instante em que ele abandona completamente a ponte?
b) Qual é o tempo gasto pelo trem para atravessar completamente a ponte?
19) O recordista mundial dos 100m rasos cumpriu o percurso num intervalo de tempo próximo a 10s. Se o movimento do corredor fosse uniformemente acelerado a partir do repouso e durante toda a corrida, sua velocidade escalar no instante da chegada seria próxima de:
a) 72 km/h
b) 54 km/h
c) 36 km/h
d) 18 km/h
e) 10 km/h
20) Numa competição automobilística, um carro se aproxima de uma curva em grande velocidade. O piloto, então, pisa no freio durante 4s e consegue reduzir a velocidade do carro para 30m/s.Durante a freada o carro percorre 160m. Supondo que os freios imprimam ao carro uma aceleração retardada constante, calcule a velocidade do carro no instante em que o piloto pisou no freio.
21) Um móvel percorre uma trajetória retilínea, em relação a um sistema de referência, com movimento uniformemente variado. Ao passar pelo ponto A, sua velocidade é de 2 m/s e, no ponto B, sua velocidade é de 6 m/s. Sabendo-se que a distancia BC é o dobro de AB, a velocidade do móvel no ponto C, em m/s, é:
A) 10
B) 12
C) 15
D) 16
E) não pode ser calculada
22) Um corpo é jogado verticalmente para cima, com velocidade inicial de 30m/s.
a) Após quanto tempo ele retorna ao solo?
b) Qual a altura atingida, em relação ao ponto de lançamento?
23) Uma partícula em queda livre em um planeta X apresenta instante $$t_{2}$$ uma velocidade de módulo 50m/s e 7,0 s depois de $$t_{2}$$, uma velocidade de módulo 120m/s. No instante $$t_{1}$$, 3,0 s antes de $$t_{2}$$, sua velocidade tinha módulo:
A) zero.
B) 10m/s
C) 20m/s
D) 30m/s
E) 40m/s
24) Um objeto é lançado, verticalmente para cima, do alto de um prédio de altura $$h_{0} = 50m$$, com uma velocidade inicial $$v_{0} = 15m/s$$.
Calcule:
a) o tempo gasto para alcançar a altura máxima.
b) a velocidade 4 s após o lançamento.
c) sua posição em relação ao nível h = 0, no instante 4s após o lançamento.
d) sua velocidade em h = 0.
25) Um paraquedista, descendo na vertical, deixou cair sua lanterna quando estava a 90m do solo. A lanterna levou 3s para atingir o solo. Qual era a velocidade do paraquedista, em m/s, quando a lanterna foi solta?
26) A distância (d) que um objeto percorre em queda livre, a partir do repouso, durante um tempo (t), é expressa por d = 0,5gt². Uma pequena esfera é solta de um ponto situado a 1,80m de altura. Calcule
a) a distância que ela percorrerá, entre os instantes t = 0,2s e t = 0,3s, contados a partir do momento em que foi solta.
b) o tempo gasto para atingir o solo.
27) Um corpo é lançado do solo verticalmente para cima. Sabe-se que, durante o decorrer do terceiro segundo do seu movimento ascendente, o móvel percorre 15m. Qual a velocidade com que o corpo foi lançado do solo?
28) Um esquiador desce por uma pista de esqui com aceleração constante. Partindo do repouso do ponto P, ele chega ao ponto T, a 100 M de P, com velocidade de 30 m/s. Com qual velocidade, em m/s, o esquiador passa por um ponto Q, a 36 m de P?
29) Um automóvel, avançando à velocidade de 36 km/h (ou 10 m/s), sofre uma colisão frontal contra um muro de concreto. Observa-se que o carro para completamente após amassar 0,50 m de sua parte frontal. A desaceleração do carro, suposta constante, durante a colisão, em m/s², é:
a) 50
b) 75
c) 100
d) 125
30) Um automóvel viaja com velocidade de 90km/h (ou seja, 25 m/s) num trecho retilíneo de uma rodovia quando, subitamente, o motorista vê um animal parado na sua pista. Entre o instante em que o motorista avista o animal e aquele começa a frear, o carro percorre 15m. Se o motorista frear o carro à taxa constante de 5 m/s², mantendo-o em sua trajetória retilínea, ele só evitará atingir o animal, que permanece imóvel durante todo o tempo, se o tiver percebido a uma distância de, no mínimo:
a) 15 m.
b) 31,25 m.
c) 52,5 m.
d) 77,5 m.
e) 125 m.
31) Um carro está a 20m de um sinal de trafego quando este passa de verde a amarelo. Supondo que o motorista acione o freio imediatamente aplicando ao carro uma desaceleração de 10m/s², calcule, em km/h, a velocidade máxima que o carro pode ter, antes de frear, para que ele pare antes cruzar o sinal.
32) Um trem de 160 metros de comprimento está parado, com a frente da locomotiva posicionada exatamente no início de uma ponte de 200 metros de comprimento, num trecho de estrada retilíneo.Num determinado instante, o trem começa a atravessar a ponte com aceleração de 0,8m/s², que se mantém constante até que ele atravesse completamente a ponte. Qual é a velocidade no instante em que ele abandona completamente a ponte?
33) Um móvel percorre uma trajetória retilínea, em relação a um sistema de referência, com movimento uniformemente variado. Ao passar pelo ponto A, sua velocidade é de 2 m/s e, no ponto B, sua velocidade é de 6 m/s. Sabendo-se que a distancia BC é o dobro de AB, a velocidade do móvel no ponto C, em m/s, é:
A) 10
B) 12
C) 15
D) 16
E) não pode ser calculada
34) Um corpo é jogado verticalmente para cima, com velocidade inicial de 30m/s. Qual a altura atingida, em relação ao ponto de lançamento?
35) Um paraquedista radical pretende atingir a velocidade do som. Para isto seu plano é saltar de um balão estacionário na alta atmosfera, equipado com roupas pressurizadas. Como nessa altitude o ar é muito rarefeito, a força de resistência do ar é desprezível. Suponha que a velocidade inicial do paraquedista em relação ao balão seja nula e que a aceleração da gravidade seja 10 m/s². A velocidade do som nessa altitude é de 300 m/s.
a) Calcule em quanto tempo ele atinge a velocidade do som.
b) Calcule a distância percorrida nesse intervalo de tempo.
36) No instante em que um corpo é arremessado para baixo, com velocidade de 10 m/s do alto de um prédio de 40 m de altura, um homem começa a correr com velocidade constante, em linha reta, para pegar o corpo rente ao chão. Sabendo que a distância do homem, no início de sua corrida, à vertical onde cai o corpo é de 10 m e que g = 10 m/s², determine a mínima velocidade do homem para alcançar o corpo.
37) Uma bola foi arremessada para cima em um planeta de gravidade desconhecida. Sabendo-se que essa bola, após 2 segundos, atingiu a altura máxima de 10m, determine a aceleração da gravidade nesse planeta.
38) Um astronauta lança, na Lua, um objeto verticalmente para cima, com velocidade inicial de 8,0 m/s. O tempo de subida até alcançar a altura máxima foi de 5,0 s. Se o lançamento do objeto fosse feito na superfície da Terra, desprezando a resistência do ar, com a mesma velocidade inicial com que foi lançado na Lua, poderíamos fazer as seguintes afirmações, EXCETO :
A) A altura máxima alcançada na Terra seria menor do que a que foi lançada na Lua.
B) O tempo de subida seria o mesmo nas duas situações.
C) O módulo da aceleração da gravidade da Lua é menor do que na Terra.
D) Na altura máxima, tanto na Lua quanto na Terra, a velocidade do objeto é nula.
39) Um automóvel percorre uma estrada em movimento uniforme variado, com função horária do espaço dada por s= t2 – 2t – 8, em unidades SI. Determine, para o móvel:
a) a função horária da velocidade.
b) o instante em que a velocidade se anula.
c) a posição no instante em que a velocidade se anula.
d) se o movimento é acelerado ou retardado em t = 3 s.
40) Um carro, partindo do repouso, assume movimento com aceleração constante de 1m/s², durante 5 segundos. Desliga-se então o motor e, devido ao atrito, o carro volta ao repouso com retardamento constante de 0,5 m/s². A duração total do movimento do corpo é de:
a) 5 segundos
b) 10 segundos
c) 15 segundos
d) 20 segundos
e) 25 segundos
41) Um móvel obedece à equação horária s = -20 + 4t – 3t², em unidades do Sistema Internacional.
a) Qual a posição inicial da partícula?
b) Qual a velocidade inicial da partícula?
c) Qual a aceleração da partícula?
42) Um automóvel percorre uma estrada em movimento uniforme variado, com função horária do espaço dada por s= t2 – 2t – 8, em unidades SI. Determine, para o móvel:
A) o espaço inicial.
B) a velocidade escalar inicial.
C) a aceleração.
D) a instante em que passa pela origem dos espaços.
E) a velocidade média entre 0 e 5s.
43) Em um teste, um automóvel acelera de 0 a 108 km/h em 10 s, em MUV. Determine a distância percorrida durante o intervalo de tempo.
44) Um móvel A parte do repouso com aceleração constante de 4m/s². No mesmo instante a 10m à frente do primeiro, um móvel B inicia um movimento uniforme com velocidade de 8m/s. Determine:
a) o instante do encontro a partir do início do movimento de ambos os corpos.
b) as distâncias percorridas por A e B até o encontro.
45) Um corpo se movimenta sobre o eixo x, com aceleração constante, de acordo com a equação horária x = 2 + 2t – 2t², em que t é dado em segundos e x em metros. Qual é a velocidade média entre os instantes t=0 e t=2 s?
46) As faixas de aceleração das autoestradas devem ser longas o suficiente para permitir que um carro, partindo do repouso, atinja a velocidade escalar de 100 km/h em uma estrada horizontal. Um carro popular é capaz de acelerar de 0 a 100 km/h em 18s. Suponha que a aceleração seja constante.
a) Qual o valor da aceleração?
b) Qual a distancia percorrida em 10s?
c) Qual deve ser o comprimento mínimo da faixa de aceleração?
47) Um carro movia-se, em linha reta, com velocidade de 20 m/s quando o motorista pisou nos freios fazendo o carro parar em 5s. A aceleração do carro nesse intervalo de tempo foi de
48) Num acelerador de partículas, uma partícula α é lançada com velocidade de $$10^{4}\, m/s$$ em trajetória retilínea no interior de um tubo. A partícula saiu do tubo com velocidade de $$9\cdot 10^{4}\, m/s$$. Sendo a aceleração constante e igual a $$10^{9}\, m/s^{2}$$, o intervalo de tempo em que a partícula permaneceu dentro do tubo foi:
a) 0,003 s
b) 0,00001 s
c) $$9\cdot 10^{-3}\, s$$
d) $$8\cdot 10^{-5}\, s$$
e) $$4\cdot 10^{-5}\, s$$
49) Uma lancha de salvamento, patrulhando a costa marítima com velocidade de 20 km/h, recebe um chamado de socorro. Verifica-se que, em 10 s, a lancha atinge a velocidade de 128 km/h. A aceleração média utilizada pela lancha foi:
a) 3,0 m/s²
b) 3,6 m/s²
c) 10,8 m/s²
d) 12,8 m/s²
e) 30 m/s²















0 comentários