Em um show de patinação no gelo, duas garotas de massas iguais giram em movimento circular uniforme em torno de uma haste vertical fixa, perpendicular ao plano horizontal. Duas fitas, $$F_{1}$$ e $$F_{2}$$, inextensíveis, de massas desprezíveis e mantidas na horizontal, ligam uma garota à outra, e uma delas à haste. Enquanto as garotas patinam, as fitas, a haste e os centros de massa das garotas mantêm-se num mesmo plano perpendicular ao piso plano e horizontal.
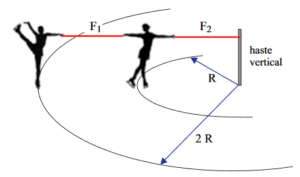
Considerando as informações indicadas na figura, que o módulo da força de tração na fita $$F_{1}$$ é igual a 120 N e desprezando o atrito e a resistência do ar, é correto afirmar que o módulo da força de tração, em newtons, na fita $$F_{2}$$ é igual a
(A) 120.
(B) 240.
(C) 60.
(D) 210.
(E) 180.
Solução:
Isolando os corpos podemos dizer que no corpo 1 \[F_{1} = F_{c1} = m\cdot \omega ^{2}\cdot 2\cdot R \longrightarrow 120 = m\cdot \omega ^{2}\cdot 2\cdot R \longrightarrow m\cdot \omega ^{2}\cdot R = 60\,\,\, (I)\] Já no corpo 2 \[F_{2} – F_{1} = F_{c2} = m\cdot\omega ^{2}\cdot R \longrightarrow F_{2} – m\cdot \omega ^{2}\cdot 2\cdot R = m\cdot\omega ^{2}\cdot R \longrightarrow F_{2} = 3\cdot m\cdot\omega ^{2}\cdot R\,\,\, (II)\] Substituindo I em II temos \[F_{2} = 3\cdot 60 \longrightarrow F_{2} = 180\, N\] Resposta: letra E.


















0 comentários