As funções trigonométricas cos(x) e sen(x) são muito estudadas no Ensino Médio. A exposição deste importante conteúdo costuma contar, nas aulas, com a apresentação de gráficos e tabelas que expõem em arcos – chamados “arcos notáveis”, como por exemplo π/3, π/4 e π/6 – os valores dessas funções.
É possível, no entanto, calcular, em outros arcos, os valores destas funções, utilizando algumas identidades trigonométricas. Considerando a relação cos(x/2) = $$\sqrt{(1+cos(x))/2}$$ e a identidade fundamental da trigonometria, é possível afirmar que o valor de sen(π/12) é
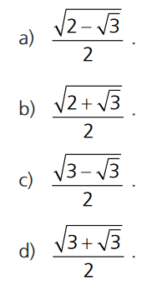
Gabarito: a)
Solução (no vídeo abaixo):

















0 comentários