Em muitos problemas cotidianos nos deparamos com a busca pelo ponto de máximo ou ponto de mínimo de uma função do segundo grau. Chamado de vértice, esse ponto (máximo ou mínimo) possui duas fórmulas bem rápidas para seu cálculo, além de terem algumas propriedades gráficas bem interessantes.
Seja uma função do tipo $$f(x) = ax^{2}+bx+c$$, as coordenadas do vértice serão
- $$X_{v} = -\frac{b}{2a}$$ e
- $$Y_{v} = -\frac{b^{2}-4ac}{4a}$$.
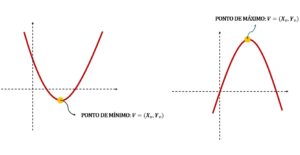
Máximo e Mínimo de uma Função do 2º Grau
Se $$a>0$$, a parábola terá concavidade voltada “para cima”; se $$a<0$$, sua concavidade será voltada “para baixo”. Isso determinará se o vértice da parábola deve ser um ponto de mínimo ou um ponto de máximo da parábola.
Exemplo
Calcule as coordenadas do vértice de x²-3x+2. Observe que esta parábola tem os parâmetros $$a=1, b-3$$ e $$c=2$$.
$$x_{v}= -\frac{3}{2\cdot 1}=-1,5$$.
$$y_{v} = -\frac{3^{2}-4\cdot 1\cdot 2}{4\cdot 1}=-\frac{1}{4}$$.
O vértice é dado por $$V=(-\frac{3}{2};-\frac{1}{4})$$. Como $$a=1>0$$, este é um ponto de mínimo.
Uma Demonstração
Usando o Cálculo Diferencial, podemos encontrar as coordenadas do vértice. De fato, quando a função é derivada e igualada a zero, encontramos o $$x$$ que maximiza ou minimiza a função. Em nosso caso, $$f(x) = ax^{2}+bx+c$$, então a derivada igualada a zero será $$f'(x) = 2ax_{v} + b=0$$, o que produz $$2ax_{v}=-b$$, logo $$x_{v} = -\frac{b}{2a}$$.
Para encontrar o $$y$$ do vértice, basta substituir a fórmula para $$x$$ do vértice na parábola original:
\[y_{v}=ax_{v}^{2}+bx_{v}+c=\]
\[y_{v}=a\cdot (-\frac{b}{2a})^{2}+b(-\frac{b}{2a})+c=\]
\[a\frac{b^{2}}{4a^{2}}-\frac{2b^{2}}{4a}+\frac{4ac}{4a}=\]
\[\frac{b^{2}-2b^{2}+4ac}{4a}= -\frac{b^{2}-4ac}{4a}.\]
















0 comentários