Uma bola de neve está se formando de tal modo que seu volume cresça a uma taxa de 8 cm³/min. Ache a taxa segundo a qual o raio está crescendo quando a bola de neve tiver 4 cm de diâmetro.
Solução:
O volume da esfera é (4/3)πr³. Assumimos que r é uma função do tempo e derivamos o volume em t, assim
\[\frac{dV }{dt}=\frac{4\pi \cdot 3r^{2}}{3}\frac{dr}{dt}= 4\pi r^{2}\frac{dr}{dt}.\]
Como a taxa de crescimento do volume é 8 cm³/min e o raio é de 2 cm (diâmetro = 4 cm), teremos
\[\frac{dV}{dr}|_{r=2} = 4\pi 2^{2}\cdot \frac{dr}{dt}=8\Longrightarrow\]
\[\frac{dr}{dt}=\frac{8}{16\pi}=\frac{1}{2\pi}\;\text{cm/min}.\]
















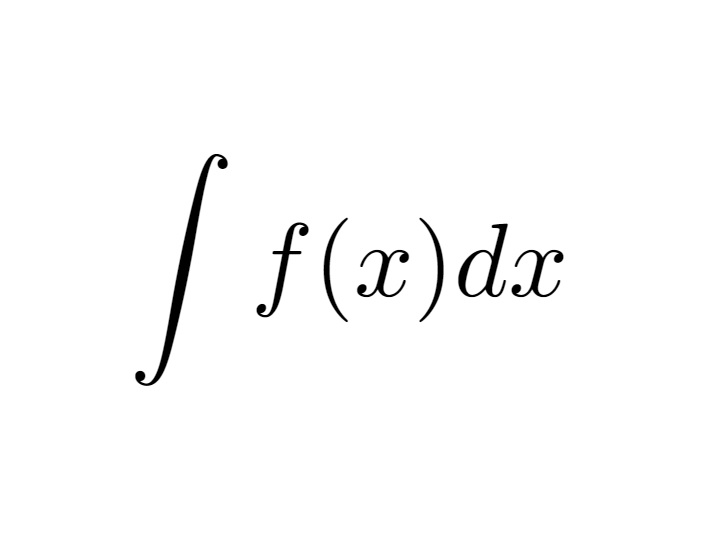
0 comentários