Exercícios sobre Vértice da Parábola

📝 Calcule o “x” e o “y” do vértice das funções a seguir:

• 4x²+x-3=0 | Solução;
• x²-2x+1 | Solução;
• -x²-10x+1 | Solução;

📝 (MACKENZIE) Uma fábrica de transportes marítimos produz x unidades mensais de um determinado modelo de lancha. Se o custo de produção é dado por C(x) = 5x²- 7x – 1  e o valor obtido na venda é dado por V(x) 4x² – x – 6, então a quantidade mensal de lanchas que devem ser vendidas de modo que se obtenha lucro máximo é
a) 15  b) 12  c) 8  d) 4  e) 3
Solução.

📝 Num terreno, na forma de um triângulo retângulo com catetos de medidas 20 e 30 metros, deseja-se construir uma casa retangular de dimensões x e y, como indicado na figura.

a) Exprima y em função de x.
b) Para que valores de x e de y a área ocupada pela casa será máxima?
Solução.

📝 (FUVEST) A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais. Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?
(A) R$ 2.000,00  (B) R$ 3.200,00  (C) R$ 3.600,00  (D) R$ 4.000,00  (E) R$ 4.800,00
Gabarito: c)
Solução

📝 O ponto de coordenadas (3, 4) pertence à parábola de equação y = ax² + bx + 4. A abscissa do vértice dessa parábola é
A) 1/2 | B) 1 | C) 3/2 | D) 2
Solução

📝 Considere um retângulo cujo perímetro é 10 cm e em que x é a medida de um dos lados. Determine:
a) a área do retângulo em função de x;
b) o valor de x para o qual a área do retângulo seja máxima.
Solução.

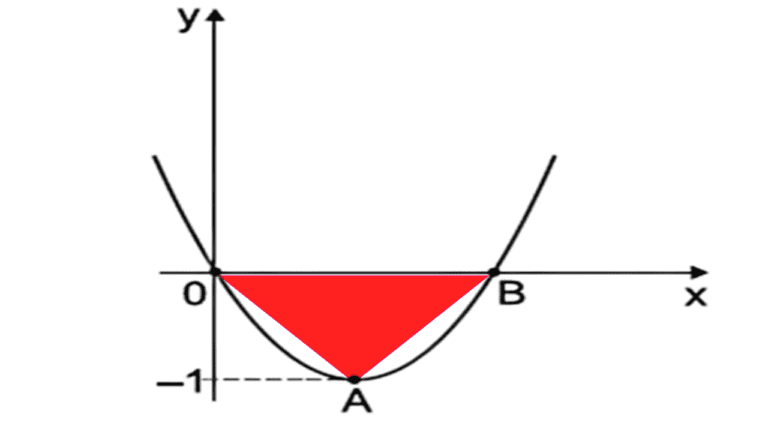
📝 No plano cartesiano, o vértice da parábola de equação y = x(1-x) e os pontos em que ela intersecta o eixo das abscissas determinam um triângulo de área igual a
a) 3/16 | b) 1/5 | c) 1/16 | d) 1/4 | e) 1/8
Gabarito: e)
Clique para ver a solução.

📝 (UNICAMP) Um jogador de futebol chuta uma bola a 30 m do gol adversário. A bola descreve uma trajetória parabólica, passa por cima da trave e cai a uma distância de 40 m de sua posição original. Se, ao cruzar a linha do gol, a bola estava a 3 m do chão, a altura máxima por ela alcançada esteve entre
a) 4,1 e 4,4 m.   b) 3,8 e 4,1 m. 
c) 3,2 e 3,5 m.  d) 3,5 e 3,8 m
Gabarito: b)
Solução (Clique aqui).

📝 (IME) Considere os triângulos ABC em que BC = 32 e AB/AC = 3. O maior valor possível para a altura relativa ao lado BC é:
(A) 8 (B) 9 (C) 10 (D) 11 (E) 12
Gabarito: e)
Solução.