Uma haste luminosa de 2,5 m de comprimento está presa verticalmente a uma boia opaca circular de 2,26 m de raio, que flutua nas águas paradas e transparentes de uma piscina, como mostra a figura. Devido à presença da boia e ao fenômeno da reflexão total da luz, apenas uma parte da haste pode ser vista por observadores que estejam fora da água.
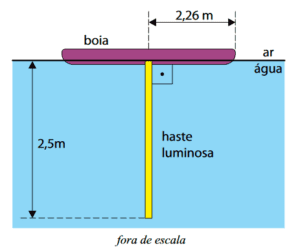
Considere que o índice de refração do ar seja 1,0, o da água da piscina $$\frac{4}{3}$$, sen 48,6º = 0,75 e tg 48,6º = 1,13. Um observador que esteja fora da água poderá ver, no máximo, uma porcentagem do comprimento da haste igual a
(A) 70%.
(B) 60%.
(C) 50%.
(D) 20%.
(E) 40%.
Confira nossa Lista de Exercícios Resolvidos de Lei de Snell e Dióptro Plano
Solução:
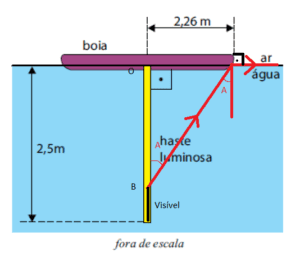
O enunciado diz que há reflexão total, logo o ângulo de saída do raio de luz é 90°. Precisamos calcular o ângulo A
\[n_{agua}\cdot sen(A) = n_{ar}\cdot sen(90^{0}) \longrightarrow \frac{4}{3}\cdot sen(A) = 1\cdot 1 \longrightarrow A = 48,6^{0}\]
Vamos Calcular agora a distância OB, não visível
\[tg(48,6^{0}) = \frac{2,26}{OB} \longrightarrow OB = 2\, m\]
Como a haste tem 2,5 m, sobra 0,5 m de haste que é visível.
\[\frac{0,5}{2,5} = 0,2 = 20%\]
Resposta: letra D.

















0 comentários