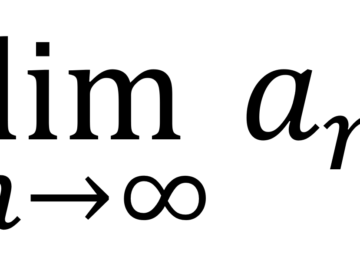Questão Seja $$\{u_{1},…,u_{n}\}\subset E$$ uma base ortonormal. Prove que, para $$v,w\in E$$ arbitrários, tem-se $$<v,w>=\sum^{n}_{i=1}<v,u_{i}>\cdot <w,u_{i}>$$. Lista de Exercícios Resolvidos sobre Produtos Internos. Solução: Escreve-se...
Sejam $$f:X \longrightarrow \mathbb{R}$$, $$a\in X’$$ e $$Y=f(X-\{a\})$$. Se $$lim_{x\to a}f(x)=L$$, então $$L\in\bar{Y}$$. Solução: Da hipótese do limite, para qualquer $$\epsilon>0$$, existe $$\delta>0$$ tal que,...
Sejam $$lim_{n\to \infty}x_{n}=a$$ e $$lim_{n\to\infty} y_{n}=b$$. Se $$a<b$$, prove que existe $$n_{0}\in\mathbb{N}$$, tal que, para todo $$n>n_{0}$$, $$x_{n}<y_{n}$$. Solução: Dado $$\epsilon>0$$, tomamos $$\epsilon/2>0$$, então existe...
Seja $$f:\mathbb{R}\longrightarrow\mathbb{R}$$ contínua. Prove que, se $$f(x)=0$$, para todo $$x\in X$$, é certo que $$f(x)=0$$, para todo $$x\in\bar{X}$$. Solução: Seja $$x\in\bar{X}$$, e seja $$f(x)=c$$. Por...
Questão 1 Suponha que o espaço vetorial de dimensão finita $$E$$ admita a decomposição $$E=\bigoplus_{j=1}^{k} F_{j}$$, como soma direta de subespaços vetoriais. Para cada $$i\in\{1,2…,k\}$$,...
Exercícios anteriores Definição \[cond_{p}(A)=||A||_{p}\cdot||A^{-1}||_{p}\]. Assumindo que $$A_{n\times n}$$ é invertível. Exercício Dadas as matrizes invertíveis $$A$$ e $$B$$ em $$\mathbb{M}_{n\times n}$$, demonstre as propriedades a...
Definição Definição de Norma vetorial \[||v||_{p}=(\sum^{n}_{i=1} |v_{i}|^{p})^{1/p}\]. Definição de Norma matricial \[||A||_{p}=\underset{||x||_{p}\neq 0}{sup}\frac{||Ax||_{p}}{||x||_{p}}\] Exercício Demonstre as propriedades da norma p, para matrizes $$A\in\mathbb{M}_{m\times n}(\mathbb{R})$$, $$B\in\mathbb{M}_{n\times...
Exercício 1 Seja uma função $$f:X\longrightarrow Y$$, e sejam $$A$$ e $$B$$ subconjuntos de $$X$$. Então $$f(A\cup B)=f(A)\cup f(B)$$. Solução (clique aqui) Exercício...
Sejam as funções $$f:A\longrightarrow B$$ e $$g:B\longrightarrow C$$. a) Prove que, se $$(g\circ f)(x)$$ é injetiva, $$f$$ é injetiva. b) Prove que, se $$(g\circ f)(x)$$...
Seja uma função $$f:A\longrightarrow B$$. a) Prove que $$f(f^{-1}(Y))\subset Y$$, para todo $$Y\subset B$$. b) Prove que $$f$$ é sobrejetora se, e somente se, $$f(f^{-1}(Y))=...
Seja uma função $$f:A\longrightarrow B$$. a) Prove que $$X\subset f^{-1}(f(X))$$, para todo $$X\subset A$$. b) Prove que a função é injetora se, e somente se,...
