Portal da Cinemática: acesse aqui!
1) As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem substituir dezenas de trabalhadores rurais, o que pode alterar de forma significativa a relação de trabalho nas lavouras de cana-de-açúcar. A pá cortadeira da máquina ilustrada na figura abaixo gira em movimento circular uniforme a uma frequência de 300 rpm. A velocidade de um ponto extremo P da pá vale
(Considere $$\pi = 3$$)

a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
2) Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas.

Um anemômetro em que a distância entre as conchas e o centro de rotação é $$r = 25\, cm$$, em um dia cuja velocidade do vento é $$v = 18\, km/h$$, teria uma frequência de rotação de
a) 3 rpm.
b) 200 rpm.
c) 720 rpm.
d) 1200 rpm.
Se necessário, considere π ≈ 3.
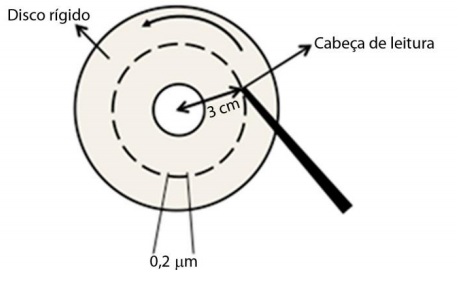
3) (UNICAMP – 2015) Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um comprimento físico de $$0,2 \mu m$$ na direção do movimento de rotação do disco. Quantas informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado apresentado abaixo? (Considere π ≈ 3.)
a) $$1,62 \cdot 10^{6}$$.
b) $$1,8 \cdot 10^{6}$$.
c) $$64,8 \cdot 10^{8}$$.
d) $$1,08 \cdot 10^{8}$$.
4) (PUCC – 2018) Para que um satélite seja utilizado para transmissões de televisão, quando em órbita, deve ter a mesma velocidade angular de rotação da Terra, de modo que se mantenha sempre sobre um mesmo ponto da superfície terrestre. Considerando R o raio da órbita do satélite, dado em km, o módulo da velocidade escalar do satélite, em km/h, em torno do centro de sua órbita, considerada circular, é
(A) $$\frac{\pi}{24} R$$.
(B) $$\frac{\pi}{12} R$$.
(C) $$\pi R$$.
(D) $$2\pi R$$.
(E) $$12\pi R$$.
5) (UNESP – 2017) Em um edifício em construção, João lança para José um objeto amarrado a uma corda inextensível e de massa desprezível, presa no ponto O da parede. O objeto é lançado perpendicularmente à parede e percorre, suspenso no ar, um arco de circunferência de diâmetro igual a 15 m, contido em um plano horizontal e em movimento uniforme, conforme a figura. O ponto O está sobre a mesma reta vertical que passa pelo ponto C, ponto médio do segmento que une João a José. O ângulo θ, formado entre a corda e o segmento de reta OC, é constante.
Considerando sen θ = 0,6, cos θ = 0,8, $$g = 10\, m/s^{2}$$ e desprezando a resistência do ar, a velocidade angular do objeto, em seu movimento de João a José, é igual a
(A) 1,0 rad/s.
(B) 1,5 rad/s.
(C) 2,5 rad/s.
(D) 2,0 rad/s.
(E) 3,0 rad/s.
6) (UNESP – 2015) A figura representa, de forma simplificada, parte de um sistema de engrenagens que tem a função de fazer girar duas hélices, $$H_{1}$$ e $$H_{2}$$. Um eixo ligado a um motor gira com velocidade angular constante e nele estão presas duas engrenagens, A e B. Esse eixo pode se movimentar horizontalmente assumindo a posição 1 ou 2. Na posição 1, a engrenagem B acopla-se à engrenagem C e, na posição 2, a engrenagem A acopla-se à engrenagem D. Com as engrenagens B e C acopladas, a hélice $$H_{1}$$ gira com velocidade angular constante $$\omega _{1}$$ e, com as engrenagens A e D acopladas, a hélice $$H_{2}$$ gira com velocidade angular constante $$\omega _{2}$$.
Considere $$r_{A}$$, $$r_{B}$$, $$r_{C}$$ e $$r_{D}$$ os raios das engrenagens A, B, C e D, respectivamente. Sabendo que $$r_{B} = 2\cdot r_{A}$$ e que $$r_{C} = r_{D}$$, é correto afirmar que a relação $$\frac{\omega _{1}}{\omega _{2}}$$ é igual a
(A) 1,0.
(B) 0,2.
(C) 0,5.
(D) 2,0.
(E) 2,2.
7) (UNESP – 2017/2) As pás de um gerador eólico de pequeno porte realizam 300 rotações por minuto. A transformação da energia cinética das pás em energia elétrica pelo gerador tem rendimento de 60%, o que resulta na obtenção de 1 500 W de potência elétrica.
Considerando π = 3, calcule o módulo da velocidade angular, em rad/s, e da velocidade escalar, em m/s, de um ponto P situado na extremidade de uma das pás, a 1,2 m do centro de rotação. Determine a quantidade de energia cinética, em joules, transferida do vento para as pás do gerador em um minuto. Apresente os cálculos.
8) (UNICAMP – 2022 – adaptada) O órgão Hammond, instrumento eletromecânico inventado por Laurens Hammond e John Hanert em 1935, como alternativa aos órgãos de tubos em igrejas, rapidamente tornou-se popular entre músicos de jazz e de outros gêneros musicais. O funcionamento do instrumento é baseado num conjunto de rodas fônicas (discos metálicos com dentes magnetizados) que giram próximas a bobinas eletromagnéticas (sensores), conforme a figura A. À medida que os dentes passam em frente ao sensor, o fluxo magnético através da bobina varia, dando origem a uma corrente elétrica que oscila com um período correspondente à passagem de cada dente. Essa corrente elétrica é então amplificada e alimenta os alto-falantes. Se a roda fônica da nota Lá, de frequência f = 220 Hz, possui 8 dentes e tem um raio R = 3,0 cm, qual é o módulo da velocidade linear de um ponto na extremidade de um dente?

















0 comentários