Portal da Ondulatória: acesse aqui!
Exercícios de Efeito Doppler, Estacionariedade, Harmônicos e Tubos (clique aqui)
Questão
(FATEC – 2018/2) Segundo o texto, a emissão de sinais da Voyager 1 leva de 12 a 14 horas para chegar à Terra. Isto se deve ao fato de que esses sinais são ondas
(A) mecânicas, que viajam a velocidades próximas da luz.
(B) mecânicas, que viajam a velocidades próximas do som.
(C) eletromagnéticas, que viajam a velocidades próximas da luz.
(D) eletromagnéticas, que viajam a velocidades próximas do som.
(E) eletromagnéticas, que viajam a velocidades próximas da Voyager 1.
Questão
(UNESP – 2017) Radares são emissores e receptores de ondas de rádio e têm aplicações, por exemplo, na determinação de velocidades de veículos nas ruas e rodovias. Já os sonares são emissores e receptores de ondas sonoras, sendo utilizados no meio aquático para determinação da profundidade dos oceanos, localização de cardumes, dentre outras aplicações. Comparando-se as ondas emitidas pelos radares e pelos sonares, temos que:
(A) as ondas emitidas pelos radares são mecânicas e as ondas emitidas pelos sonares são eletromagnéticas.
(B) ambas as ondas exigem um meio material para se propagarem e, quanto mais denso for esse meio, menores serão suas velocidades de propagação.
(C) as ondas de rádio têm oscilações longitudinais e as ondas sonoras têm oscilações transversais.
(D) as frequências de oscilação de ambas as ondas não dependem do meio em que se propagam.
(E) a velocidade de propagação das ondas dos radares pela atmosfera é menor do que a velocidade de propagação das ondas dos sonares pela água.
Questão
(ENEM – 2016) O morcego emite pulsos de curta duração de ondas ultrassônicas, os quais voltam na forma de ecos após atingirem objetos no ambiente, trazendo informações a respeito das suas dimensões, suas localizações e dos seus possíveis movimentos. Isso se dá em razão da sensibilidade do morcego em detectar o tempo gasto para os ecos voltarem, bem como das pequenas variações nas frequências e nas intensidades dos pulsos ultrassônicos. Essas características lhe permitem caçar pequenas presas mesmo quando estão em movimento em relação a si. Considere uma situação unidimensional em que uma mariposa se afasta, em movimento retilíneo e uniforme, de um morcego em repouso. A distância e velocidade da mariposa, na situação descrita, seriam detectadas pelo sistema de um morcego por quais alterações nas características dos pulsos ultrassônicos?
A) Intensidade diminuída, o tempo de retorno aumentado e a frequência percebida diminuída.
B) Intensidade aumentada, o tempo de retorno diminuído e a frequência percebida diminuída.
C) Intensidade diminuída, o tempo de retorno diminuído e a frequência percebida aumentada.
D) Intensidade diminuída, o tempo de retorno aumentado e a frequência percebida aumentada.
E) Intensidade aumentada, o tempo de retorno aumentado e a frequência percebida aumentada.
Questão
(FATEC – 2019) No curso de “Big Data no Agronegócio” da FATEC, o aluno estuda sobre eletrônica, circuitos eletrônicos e suas propriedades, tais como ondas que podem ser registradas em um osciloscópio. A figura representa duas dessas ondas que se propagam em sentidos opostos e com mesma velocidade de módulo $$2\cdot 10^{-6}\, m/s$$.
Considerando a situação apresentada pela figura no instante t = 0, podemos afirmar que, após
(A) 1 segundo, a superposição das ondas 1 e 2 apresenta uma nova onda com amplitude de 1 volt.
(B) 1 segundo, ocorre uma interferência destrutiva total.
(C) o cruzamento das ondas, a onda 2 é completamente amortecida.
(D) o cruzamento das ondas, a amplitude da onda 2 fica maior que a da onda 1.
(E) o cruzamento das ondas, a frequência da onda 1 fica maior que a da onda 2.
Questão
(ENEM – 2015) Ao ouvir uma flauta e um piano emitindo a mesma nota musical, consegue-se diferenciar esses instrumentos um do outro. Essa diferenciação se deve principalmente ao(à)
A) intensidade sonora do som de cada instrumento musical.
B) potência sonora do som emitido pelos diferentes instrumentos musicais.
C) diferente velocidade de propagação do som emitido por cada instrumento musical.
D) timbre do som, que faz com que os formatos das ondas de cada instrumento sejam diferentes.
E) altura do som, que possui diferentes frequências para diferentes instrumentos musicais.
Questão
(UNESP – 2016) Uma corda elástica está inicialmente esticada e em repouso, com uma de suas extremidades fixa em uma parede e a outra presa a um oscilador capaz de gerar ondas transversais nessa corda. A figura representa o perfil de um trecho da corda em determinado instante posterior ao acionamento do oscilador e um ponto P que descreve um movimento harmônico vertical, indo desde um ponto mais baixo (vale da onda) até um mais alto (crista da onda).
Sabendo que as ondas se propagam nessa corda com velocidade constante de 10 m/s e que a frequência do oscilador também é constante, a velocidade escalar média do ponto P, em m/s, quando ele vai de um vale até uma crista da onda no menor intervalo de tempo possível é igual a
(A) 4.
(B) 8.
(C) 6.
(D) 10.
(E) 12.
Questão
(UNICAMP – 2014) A tecnologia de telefonia celular 4G passou a ser utilizada no Brasil em 2013, como parte da iniciativa de melhoria geral dos serviços no Brasil, em preparação para a Copa do Mundo de 2014. Algumas operadoras inauguraram serviços com ondas eletromagnéticas na frequência de 40 MHz. Sendo a velocidade da luz no vácuo $$c = 3\cdot 10^{8}\, m/s$$, o comprimento de onda dessas ondas eletromagnéticas é
a) 1,2 m.
b) 7,5 m.
c) 5,0 m.
d) 12,0 m.
Questão
(UNICAMP – 2017) Considere que, de forma simplificada, a resolução máxima de um microscópio óptico é igual ao comprimento de onda da luz incidente no objeto a ser observado. Observando a célula representada na figura abaixo, e sabendo que o intervalo de frequências do espectro de luz visível está compreendido entre $$4,0\cdot 10^{14}\, Hz$$ e $$7,5\cdot 10^{14}\, Hz$$, a menor estrutura celular que se poderia observar nesse microscópio de luz seria
(Se necessário, utilize $$c = 3\cdot 10^{8}\, m/s$$.)
a) o ribossomo.
b) o retículo endoplasmático.
c) a mitocôndria.
d) o cloroplasto.
Questão
(UERJ – 2018) Em uma antena de transmissão, elétrons vibram a uma frequência de $$3\cdot 10^{6}\, Hz$$. Essa taxa produz uma combinação de campos elétricos e magnéticos variáveis que se propagam como ondas à velocidade da luz. No diagrama abaixo, estão relacionados tipos de onda e seus respectivos comprimentos.
Com base nessas informações, identifique o tipo de onda que está sendo transmitida pela antena na frequência mencionada, justificando sua resposta a partir dos cálculos.
Questão
(PUC-Campinas – 2018) O som do rádio chega até nós codificado nas ondas eletromagnéticas emitidas pelas antenas das emissoras. Sabendo que 1 MHz é igual a $$10^{6}\, Hz$$ e considerando a velocidade de propagação das ondas eletromagnéticas no ar igual a $$3,0\cdot 10^{8}\, m/s$$, o comprimento de onda e o período das ondas emitidas por uma emissora de rádio que opera com frequência de 100 MHz são, respectivamente,
(A) 1,0 m e $$1,0\cdot 10^{-8}\, s$$.
(B) 1,0 m e $$3,0\cdot 10^{-8}\, s$$.
(C) 3,0 m e $$1,0\cdot 10^{-6}\, s$$.
(D) 3,0 m e $$3,0\cdot 10^{-6}\, s$$.
(E) 3,0 m e $$1,0\cdot 10^{-8}\, s$$.
Questão
(UNESP – 2013) A imagem, obtida em um laboratório didático, representa ondas circulares produzidas na superfície da água em uma cuba de on- das e, em destaque, três cristas dessas ondas. O centro gerador das ondas é o ponto P, perturbado periodicamente por uma haste vibratória.
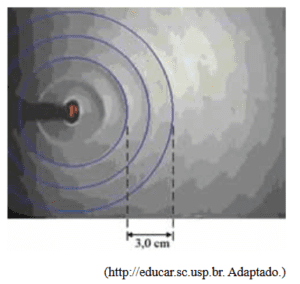
Considerando as informações da figura e sabendo que a velocidade de propagação dessas ondas na superfície da água é 13,5 cm/s, é correto afirmar que o número de vezes que a haste toca a superfície da água, a cada segundo, é igual a
(A) 1,5.
(B) 9,0.
(C) 13,5.
(D) 4,5.
(E) 3,0.
Questão
(ENEM – 2015) A radiação ultravioleta (UV) é dividida, de acordo com três faixas de frequência, em UV-A, UV-B e UV-C, conforme a figura.
Para selecionar um filtro solar que apresente absorção máxima na faixa UV-B, uma pessoa analisou os espectros de absorção da radiação UV de cinco filtros solares:
Considere:
velocidade da luz = $$3,0\cdot 10^{8}\, m/s$$ e 1 nm = $$1,0\cdot 10^{-9}\, m$$.
O filtro solar que a pessoa deve selecionar é o
A) V.
B) IV.
C) III.
D) II.
E) I.
Questão
(UNICAMP – 2014) A figura abaixo mostra o esquema de um forno de micro-ondas, com 30 cm de distância entre duas de suas paredes internas paralelas, assim como uma representação simplificada de certo padrão de ondas estacionárias em seu interior. Considere a velocidade das ondas no interior do forno como $$c=3⋅10^8 m/s$$ e calcule a frequência f das ondas que formam o padrão representado na figura.
Questão
(ENEM – 2018) O sonorizador é um dispositivo físico implantado sobre a superfície de uma rodovia de modo que provoque uma trepidação e ruído quando da passagem de um veículo sobre ele, alertando para uma situação atípica à frente, como obras, pedágios ou travessia de pedestres. Ao passar sobre os sonorizadores, a suspensão do veículo sofre vibrações que produzem ondas sonoras, resultando em um barulho peculiar. Considere um veículo que passe com velocidade constante igual a 108 km/h sobre um sonorizador cujas faixas são separadas por uma distância de 8 cm. A frequência da vibração do automóvel percebida pelo condutor durante a passagem nesse sonorizador é mais próxima de
a)8,6 Hz
b)13,5 Hz
c)375 Hz
d)1350 Hz
e)4860 Hz
Questão
(FUVEST – 2015) A figura acima mostra parte do teclado de um piano. Os valores das frequências das notas sucessivas, incluindo os sustenidos, representados pelo símbolo #, obedecem a uma progressão geométrica crescente da esquerda para a direita; a razão entre as frequências de duas notas Dó consecutivas vale 2; a frequência da nota Lá do teclado da figura é 440 Hz. O comprimento de onda, no ar, da nota Sol indicada na figura é próximo de
a) 0,56 m
b) 0,86 m
c) 1,06 m
d) 1,12 m
e) 1,45 m
Note e adote:
$$2^{1/12}=1,059$$
$$(1,059)^{2}=1,12$$
velocidade do som no ar=340 m/s
Questão
(FUVEST – 2016 – adaptada) Lasers pulsados de altíssima potência estão sendo construídos na Europa. Esses lasers emitirão pulsos de luz verde, e cada pulso terá $$10^{15}$$ W de potência e duração de cerca de $$30\cdot 10^{-15}$$ s. Com base nessas informações, determine o comprimento de onda λ da luz desse laser;
Questão
(UEL) Numa corda, uma fonte de ondas realiza um movimento vibratório com frequência de 10 Hz. O diagrama mostra, num determinado instante, a forma da corda percorrida pela onda.
A velocidade de propagação da onda, em cm/s, é de
a) 8,0
b) 20
c) 40
d) 80
e) 160
Questão
(UFG) O gráfico do movimento de subida e descida de uma rolha, na superfície de um lago ondulado, é mostrado na figura a seguir, em que y é a altura da rolha em relação ao nível da água parada, e t é o tempo transcorrido.
Se a rolha leva 1,0 s para sair do nível zero e atingir, pela primeira vez, a altura máxima, a frequência do movimento é igual a:
a) 0,125 Hz.
b) 0,25 Hz.
c) 0,50 Hz.
d) 1,0 Hz.
e) 4,0 Hz.
Questão
(UNESP 2015) A figura representa ondas chegando a uma praia. Observa-se que, à medida que se aproximam da areia, as cristas vão mudando de direção, tendendo a ficar paralelas à orla. Isso ocorre devido ao fato de que a parte da onda que atinge a região mais rasa do mar tem sua velocidade de propagação diminuída, enquanto a parte que se propaga na região mais profunda permanece com a mesma velocidade até alcançar a região mais rasa, alinhando-se com a primeira parte.
O que foi descrito no texto e na figura caracteriza um fenômeno ondulatório chamado
(A) reflexão.
(B) difração.
(C) refração.
(D) interferência.
(E) polarização.
Questão
(UNESP 2022) Quando uma onda se propaga por águas rasas, isto é, onde a profundidade é menor do que metade do comprimento da onda, sua velocidade de propagação pode ser calculada com a expressão $$v = \sqrt{g\times h}$$, em que g é a aceleração da gravidade local e h a profundidade das águas na região. Dessa forma, se uma onda passar de uma região com certa profundidade para outra com profundidade diferente, ela sofrerá variação em sua velocidade de propagação, o que caracteriza o fenômeno de refração dessa onda. A figura mostra uma mesma onda propagando-se por uma região de profundidade $$h_{1} = 3,6\, m$$ com comprimento de onda $$\lambda_{1} = 12\, m$$ e, em seguida, propagando-se por uma região de profundidade $$h_{2} = 0,9\, m$$ com comprimento de onda $$\lambda_{2}$$.
Na situação apresentada, o comprimento de onda $$\lambda_{2}$$ é
(A) 6 m.
(B) 2 m.
(C) 8 m.
(D) 1 m.
(E) 4 m.
Questão
(UNESP 2022) Nossos olhos percebem, apenas, uma pequena faixa do espectro eletromagnético, chamada de luz visível. Outras faixas dessa radiação podem ser detectadas por instrumentos específicos. No espaço extraterrestre, partículas de alta energia produzidas em todo o universo se propagam e, normalmente, são bloqueadas por campos magnéticos. Porém, como a Lua não possui campo magnético, essas partículas atingem a superfície lunar, interagem com a matéria e produzem raios gama como resultado, que podem ser detectados na Terra. A figura da esquerda mostra uma imagem da Lua obtida na faixa da luz visível e, a da direita, obtida na faixa dos raios gama.
Comparando os raios de luz visível com os raios gama, é correto afirmar que:
(A) como todas as ondas eletromagnéticas, ambos só podem se propagar pelo vácuo, e com velocidades iguais.
(B) por apresentarem comprimentos de onda maiores do que os da luz visível, os raios gama são inofensivos quando atingem os seres humanos.
(C) os raios gama apresentam frequências menores do que as da luz visível, o que explica terem velocidade de propagação maior do que essa luz, no vácuo.
(D) provenientes simultaneamente de uma mesma fonte no espaço, ambos chegam à Terra em intervalos de tempo diferentes, produzindo imagens distintas dessa fonte.
(E) apesar de terem frequências e comprimentos de onda diferentes, ambos se propagam pelo vácuo com velocidades iguais.
Questão
(ENEM 2016) Um experimento para comprovar a natureza ondulatória da radiação de micro-ondas foi realizado da seguinte forma: anotou-se a frequência de operação de um forno de micro-ondas e, em seguida, retirou-se sua plataforma giratória. No seu lugar, colocou-se uma travessa refratária com uma camada grossa de manteiga. Depois disso, o forno foi ligado por alguns segundos. Ao se retirar a travessa refratária do forno, observou-se que havia três pontos de manteiga derretida alinhados sobre toda a travessa. Parte da onda estacionária gerada no interior do forno é ilustrada na figura.
De acordo com a figura, que posições correspondem a dois pontos consecutivos da manteiga derretida?
A) I e III
B) I e V
C) II e III
D) II e IV
E) II e V
Questão
(UNESP 2022) Duas pessoas estão paradas de frente e à mesma distância de uma parede vertical, segurando, cada uma, a extremidade de uma corda elástica, que tem a outra extremidade fixa nessa parede, na posição horizontal e em repouso. Simultaneamente, essas pessoas começam a fazer essas cordas oscilarem e, em um mesmo intervalo de tempo, as duas cordas assumem as configurações mostradas nas figuras 1 e 2.
Sendo $$v_{1}$$ e $$v_{2}$$ as velocidades de propagação das ondas nas cordas nas figuras 1 e 2, respectivamente, temos que:
(A) $$v_{2} = 1,0\cdot v_{1}$$
(B) $$v_{2} = 0,6\cdot v_{1}$$
(C) $$v_{2} = 0,8\cdot v_{1}$$
(D) $$v_{2} = 1,2\cdot v_{1}$$
(E) $$v_{2} = 1,6\cdot v_{1}$$
Questão
(UNESP 2021) O efeito fotoelétrico é um processo em que ocorre a emissão de elétrons por uma placa metálica, chamados fotoelétrons, quando a radiação eletromagnética incide sobre ela com uma quantidade de energia suficiente para removê-los da superfície da placa. A quantidade mínima dessa energia que remove cada elétron é chamada função trabalho do metal (Φ). No estudo desse efeito, considera-se que a energia (ε) associada a um fóton de determinada radiação que se propaga com frequência f é dada pela expressão ε = h × f, em que h é uma constante positiva. Nesse processo, essa energia é totalmente absorvida por um elétron ligado à placa, sendo parte utilizada para removê-lo do metal e o restante transformada em energia cinética desse fotoelétron ($$E_{cin}$$ = ε – Φ).
A tabela apresenta as funções trabalho do sódio e do alumínio, expressas em joules.
Considere que uma radiação ultravioleta de comprimento de onda $$\lambda = 4\times 10^{-7}\, m$$, propagando-se no vácuo, incida sobre duas placas, uma feita de sódio e outra de alumínio. Sendo a velocidade da luz no vácuo $$c = 3\times 10^{8}\, m/s$$ e adotando-se $$h = 6,4\times 10^{-34}\, J\cdot s$$, nessa situação somente a placa de
(A) alumínio emitirá fotoelétrons, cada um com $$2,0\times 10^{-19}\, J$$ de energia cinética.
(B) alumínio emitirá fotoelétrons, cada um com $$2,4\times 10^{-19}\, J$$ de energia cinética.
(C) sódio emitirá fotoelétrons, cada um com $$2,4\times 10^{-19}\, J$$ de energia cinética.
(D) sódio emitirá fotoelétrons, cada um com $$1,1\times 10^{-19}\, J$$ de energia cinética.
(E) alumínio emitirá fotoelétrons, cada um com $$1,1\times 10^{-19}\, J$$ de energia cinética.
Questão
(FUVEST – 2022 – adaptada) A conversão de energia mecânica das ondas do mar é uma promissora fonte alternativa de energia limpa, e vários protótipos têm sido desenvolvidos para este fim. Uma das possíveis aplicações é o uso de câmaras de ar pressurizadas que usem a oscilação das ondas do mar para fazer girar o eixo de um dínamo ou de uma turbina, gerando energia elétrica. Considere o esquema mostrado na figura: uma boia flutua no mar e seu movimento vertical faz mover o pistão 1 de área A que comprime o ar em uma câmara pressurizada a uma pressão $$P_{0}$$. A distância máxima entre o pistão 1 e o topo da câmara é L. Um segundo pistão (pistão 2) de área A/10 colocado horizontalmente na lateral superior da câmara é acoplado a um mecanismo que faz girar um dínamo. Considere inicialmente que ambos os pistões são livres para se movimentarem sem atrito e que a pressão e a temperatura do gás no interior da câmara não se alterem significativamente.
Se as ondas do mar forem ondas perfeitamente harmônicas com velocidade de 3 m/s e a distância entre as cristas for de 5 m, calcule o período de rotação do dínamo.
Questão
(FATEC – 2017/2) Um aluno do curso de Cosméticos da FATEC trabalha em uma indústria farmacêutica fazendo aprimoramento de Filtros Solares Físicos e Químicos (FSF e FSQ, respectivamente). Para isso, ele estuda as radiações solares chamadas de UVA e UVB, montando um quadro esquemático.
Baseando-se nas informações apresentadas no quadro, é certo afirmar que
(A) a radiação UVA possui menor comprimento de onda e produz os mesmos efeitos que a UVB.
(B) as duas radiações não são igualmente penetrantes e não são refletidas por FSF.
(C) as duas radiações penetram as mesmas camadas da pele e são absorvidas por FSQ.
(D) a radiação UVA apresenta maior frequência e é mais penetrante que a UVB.
(E) a radiação UVB apresenta maior frequência e menor comprimento de onda que a UVA.
Questão
(ENEM – 2021) O sino dos ventos é composto por várias barras metálicas de mesmo material e espessura, mas de comprimentos diferentes, conforme a figura.
Considere $$f_{1}$$ e $$v_{1}$$, respectivamente, como a frequência fundamental e a velocidade de propagação do som emitido pela barra de menor comprimento, e $$f_{2}$$ e $$v_{2}$$ são essas mesmas grandezas para o som emitido pela barra de maior comprimento.
As relações entre as frequências fundamentais e entre as velocidades de propagação são, respectivamente,
a) $$f_{1} < f_{2}$$ e $$v_{1} < v_{2}$$
b) $$f_{1} < f_{2}$$ e $$v_{1} = v_{2}$$
c) $$f_{1} < f_{2}$$ e $$v_{1} > v_{2}$$
d) $$f_{1} > f_{2}$$ e $$v_{1} = v_{2}$$
e) $$f_{1} > f_{2}$$ e $$v_{1} > v_{2}$$


















0 comentários