$$\int x\cdot e^{x^{2}}dx$$.
Temos a nossa $$f(x)=x\cdot e^{x^{2}}=x\cdot e^{g(x)}$$. Nossa função auxiliar é $$u=g(x)=x^{2}$$.
Portanto já sabemos que $$\frac{du}{2x}=dx$$, pois adotamos os mesmos passos do Agora, basta aplicar na fórmula que vimos.
\[\int x\cdot e^{x^{2}}dx=\int x\cdot e^{u}\frac{du}{2x}=\int\frac{1}{2}e^{u}du=(1/2)e^{u}+K=(1/2)e^{x^{2}}+K\].
















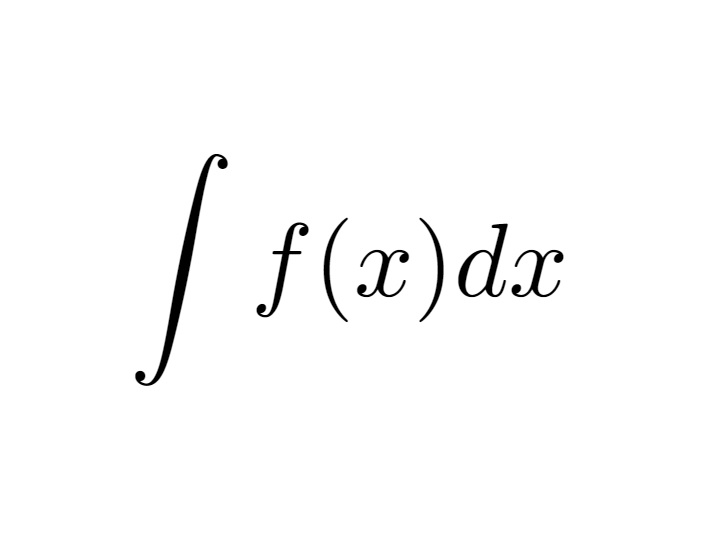
0 comentários