Vamos calcular $$\int x sec^{2}(x)dx$$.
Solução:
Se tomarmos $$u=x$$ e $$dv = sec^{2}(x) dx$$, a função $$v(x)$$ é claramente igual à tangente de x, pois $$tg(x)’ = sec^{2}(x)$$. Então a integração por partes fornece
\[\int x sec^{2}(x)dx= xtg(x)-\int (x)’tg(x)dx = \]
\[xtg(x)-\int tg(x)dx.\]
Observe que a última integral tem resultado igual a $$Ln(cos(x)) + K$$. Desse modo, teremos
\[\int x\cdot sec^{2}(x)dx = x\cdot tg(x) + Ln(cos(x)) + K.\]
















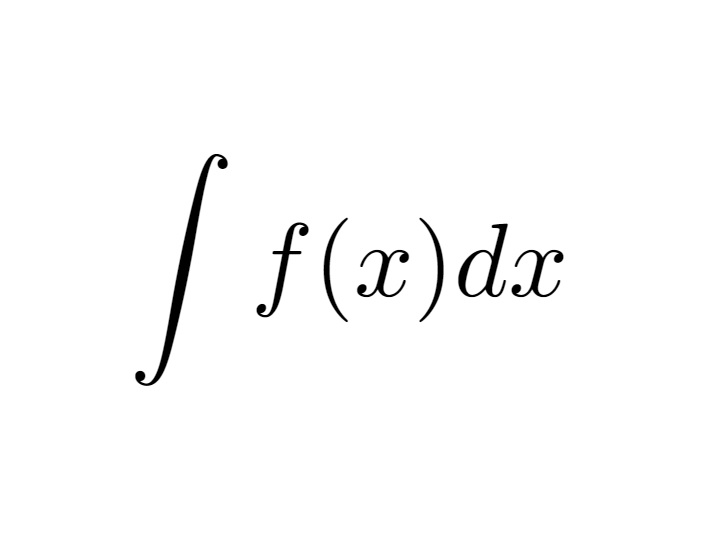
0 comentários