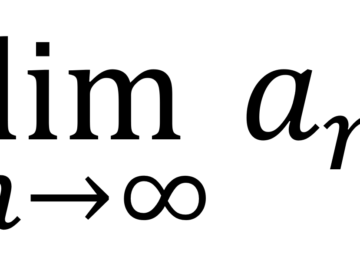Sejam $$lim_{n\to \infty}x_{n}=a$$ e $$lim_{n\to\infty} y_{n}=b$$. Se $$a<b$$, prove que existe $$n_{0}\in\mathbb{N}$$, tal que, para todo $$n>n_{0}$$, $$x_{n}<y_{n}$$. Solução: Dado $$\epsilon>0$$, tomamos $$\epsilon/2>0$$, então existe...
Demonstre, pela definição ε-δ, que o limite existe e tem o valor designado, no ponto dado. $$\lim_{x\to 3}(2x+4)=10$$. Lista de Exercícios Resolvidos sobre Limites, acesse...
Sejam $$f$$ e $$g$$ duas funções tais que a imagem da $$f$$ é um subconjunto do domínio da $$g$$. Se $$g$$ é uma função contínua...
Sejam duas funções (f,g), definidas nos reais, tais que , $$g(x)\neq 0$$, em todo do domínio. Suponha que $$lim_{x\to p}\frac{f(x)}{g(x)}=0$$. Prove que existe um δ>0...
Demonstre, pela definição ε-δ, que o limite existe e tem o valor designado, no ponto dado. $$\lim_{x\to 4}(x-1)=3$$ Lista de Exercícios Resolvidos sobre Limites, acesse...
Caso exista, calcule o limite da sequência $$\frac{(-1)^{n}}{n}+2$$. Solução: Observe que a sequência é $$2-1 ; 2+\frac{1}{2} ; 2 – \frac{1}{3},…$$. Apesar de sua alternância,...
Prove que limx→0+ 1/ (1+a1/x) =0. Solução:
Prove que o limite abaixo existe e calcule o valor. \[\lim_{(x,y)\to (0,0)}\frac{x^{2}-y^{2}}{1+x^{2}+y^{2}}\]
Motivação e Definição de Limite Neste artigo, estudamos as principais propriedades do limite que tende ao infinito. Se tomarmos como exemplo a função $$f(x)=\frac{1}{x}$$, definida...
