1) As figuras 1 e 2 representam uma pessoa segurando uma pedra de 12 kg e densidade $$2\cdot 10^{3}\, kg/m^{3}$$, ambas em repouso em relação à água de um lago calmo, em duas situações diferentes. Na figura 1, a pedra está totalmente imersa na água e, na figura 2, apenas um quarto dela está imerso. Para manter a pedra em repouso na situação da figura 1, a pessoa exerce sobre ela uma força vertical para cima, constante e de módulo $$F_{1}$$. Para mantê-la em repouso na situação da figura 2, exerce sobre ela uma força vertical para cima, constante e de módulo $$F_{2}$$.
Considerando a densidade da água igual a $$10^{3}\, kg/m^{3}$$ e $$g = 10 m/s^{2}$$, é correto afirmar que a diferença $$F_{2} – F_{1}$$, em newtons, é igual a
(A) 60.
(B) 75.
(C) 45.
(D) 30.
(E) 15.
2) Algumas embalagens trazem, impressas em sua superfície externa, informações sobre a quantidade máxima de caixas iguais a ela que podem ser empilhadas, sem que haja risco de danificar a embalagem ou os produtos contidos na primeira caixa da pilha, de baixo para cima. Considere a situação em que três caixas iguais estejam empilhadas dentro de um elevador e que, em cada uma delas, esteja impressa uma imagem que indica que, no máximo, seis caixas iguais a ela podem ser empilhadas.
Suponha que esse elevador esteja parado no andar térreo de um edifício e que passe a descrever um movimento uniformemente acelerado para cima. Adotando $$g = 10 m/s^{2}$$, é correto afirmar que a maior aceleração vertical que esse elevador pode experimentar, de modo que a caixa em contato com o piso receba desse, no máximo, a mesma força que receberia se o elevador estivesse parado e, na pilha, houvesse seis caixas, é igual a
(A) $$4 m/s^{2}$$.
(B) $$8 m/s^{2}$$.
(C) $$10 m/s^{2}$$.
(D) $$6 m/s^{2}$$.
(E) $$2 m/s^{2}$$.
3) Uma boia de sinalização marítima muito simples pode ser construída unindo-se dois cilindros de mesmas dimensões e de densidades diferentes, sendo um de densidade menor e outro de densidade maior que a da água, tal como esquematizado na figura abaixo. Submergindo-se totalmente esta boia de sinalização na água, quais serão os pontos efetivos mais prováveis de aplicação das forças Peso e Empuxo?
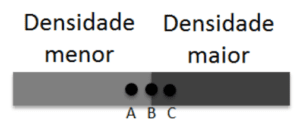
a) Peso em C e Empuxo em B.
b) Peso em B e Empuxo em B.
c) Peso em C e Empuxo em A.
d) Peso em B e Empuxo em C.
4)
A barra da figura acima é homogênea, possui massa m = 30 kg e comprimento L = 4,0 m. Ela está apoiada sobre o ponto A em um plano horizontal rugoso e é vinculada pelo ponto C, a um metro de topo da barra, a uma mola de constante elástica K. Sabe-se que o campo gravitacional local tem módulo $$g=10\, m/s^{2}$$ e que o sistema encontra-se em equilíbrio quando Ө = 45º e a mola tem sua extensão máxima $$x_{m\acute{a} x} = 0,20\, m$$. Com base nos dados fornecidos, pode-se afirmar que o valor de K, em kN/m, é
a) 5,0
b) 4,0
c) 3,0
d) 2,0
e) 1,0
5) Um homem de 50 kg está sobre uma balança graduada em newtons, no interior de um elevador. Determine:
a) a indicação da balança quando o elevador sobe com aceleração constante de 2 m/s².
b) o módulo e o sentido da aceleração do elevador quando a balança marca 450 N.
6) Em uma obra, para permitir o transporte de objetos para cima, foi montada uma máquina constituída por uma polia, fios e duas plataformas A e B horizontais, todos de massas desprezíveis, como mostra a figura. Um objeto de massa m = 225 kg, colocado na plataforma A, inicialmente em repouso no solo, deve ser levado verticalmente para cima e atingir um ponto a 4,5 m de altura, em movimento uniformemente acelerado, num intervalo de tempo de 3 s. A partir daí, um sistema de freios passa a atuar, fazendo a plataforma A parar na posição onde o objeto será descarregado.
Considerando g = 10 m/s², desprezando os efeitos do ar sobre o sistema e os atritos durante o movimento acelerado, a massa M, em kg, do corpo que deve ser colocado na plataforma B para acelerar para cima a massa m no intervalo de 3 s é igual a
(A) 275.
(B) 285.
(C) 295.
(D) 305.
(E) 315.

















0 comentários