Trigonometria no Triângulo Retângulo – Exercícios Resolvidos

Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é…
Solução.

Um triângulo retângulo tem a hipotenusa e um dos catetos medindo, respectivamente, 2√3 cm e 3 cm. A medida do ângulo oposto ao cateto dado é…
Solução.

Em um triângulo retângulo, a medida da hipotenusa é o dobro da medida de um dos catetos. O ângulo oposto ao menor lado desse triângulo mede…
Solução.

(UNICAMP – 2013) Ao decolar, um avião deixa o solo com um ângulo constante de 15º. A 3,8 km da cabeceira da pista existe um morro íngreme. A figura abaixo ilustra a decolagem, fora de escala. Podemos concluir que o avião ultrapassa o morro a uma altura, a partir da sua base, de

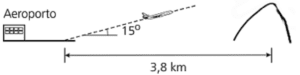
a) 3,8 tan (15°) km.
b) 3,8 sen (15°) km.
c) 3,8 cos (15°) km.
d) 3,8 sec (15°) km.
Solução

(FEI) Dado o trapézio conforme a figura a seguir, o valor do seno do ângulo α é…
Dados: AE = 1 cm,  BC = 2 cm, CF = 4 cm e α = CAD.
Solução

(UEMG – 2016) Observe a figura:

Tendo como vista lateral da escada com 6 degraus, um triângulo retângulo isósceles de hipotenusa √10 metros, Magali observa que todos os degraus da escada têm a mesma altura. A medida em cm, de cada degrau, corresponde aproximadamente a:
a) 37.
b) 60.
c) 75.
d) 83.
Solução

(FAAP) No triângulo retângulo ABC a seguir, têm-se AB = 8 cm e BC = 10 cm. Sendo AD a altura relativa à hipotenusa BC, calcule AD e AC.
Solução.

(PUC-Campinas – 2016/2) A figura mostra o ângulo de visão que um mesmo observador tem de uma estrutura de caixa d’água em dois pontos diferentes. Sabe-se que a altura dos olhos, em relação ao piso plano sobre o qual a estrutura está apoiada perpendicularmente, é exatamente a metade da altura da estrutura da caixa d’água, e que a distância entre os dois pontos de observação é de 2 metros.

A partir dessas informações, é possível determinar que a altura da estrutura da caixa d’água, em metros, é igual a

Solução

(UNIFENAS) Observe a figura, onde B = 60º, C= 45º e AB = 2m. O lado a do triângulo ABC é:
Solução.

(MACKENZIE) Observando o triângulo da figura, podemos afirmar que (cos⁡(𝛼)−𝑠𝑒𝑛(𝛼))/(1−tg⁡(𝛼)) vale
Solução.

(UNICAMP – 2020) A figura abaixo exibe o triângulo retângulo 𝐴𝐵𝐶, em que AB=AM=MC. Então, tg⁡θ é igual a…
Solução.

(UNICAMP – 2014) Considere um hexágono, como o exibido na figura abaixo, com cinco lados com comprimento de e um lado com comprimento de x cm. a) Encontre o valor de x. b) Mostre que a medida do ângulo α é inferior a 150º.
Solução

(UNESP – 2012/2) Um prédio hospitalar está sendo construído em um terreno declivoso. Para otimizar a construção, o arquiteto responsável idealizou o estacionamento no subsolo do prédio, com entrada pela rua dos fundos do terreno. A recepção do hospital está 5 metros acima do nível do estacionamento, sendo necessária a construção de uma rampa retilínea de acesso para os pacientes com dificuldades de locomoção.

A figura representa esquematicamente esta rampa (r), ligando o ponto A, no piso da recepção, ao ponto B, no piso do estacionamento, a qual deve ter uma inclinação α mínima de 30º e máxima de 45º. Nestas condições e considerando √2≅ 1,4 , quais deverão ser os valores máximo e mínimo, em metros, do comprimento desta rampa de acesso? 
Solução