1) Uma garota de 50 kg está brincando em um balanço constituído de um assento e de uma corda ideal que tem uma de suas extremidades presa nesse assento e a outra, em um saco de areia de 66 kg que está apoiado, em repouso, sobre o piso horizontal. A corda passa por duas roldanas ideais fixas no teto e, enquanto oscila, a garota percorre uma trajetória circular contida em um plano vertical de modo que, ao passar pelo ponto A, a corda fica instantaneamente vertical.
Desprezando a resistência do ar e a massa do assento, considerando $$g = 10\, m/s^{2}$$ e as informações contidas na figura, a maior velocidade, em m/s, com a qual a garota pode passar pelo ponto A sem que o saco de areia perca contato com o solo é igual a
(A) 2.
(B) 5.
(C) 3.
(D) 4.
(E) 1.
2) Espectrometria de massas é uma técnica instrumental que envolve o estudo, na fase gasosa, de moléculas ionizadas, com diversos objetivos, dentre os quais a determinação da massa dessas moléculas. O espectrômetro de massas é o instrumento utilizado na aplicação dessa técnica.
(www.em.iqm.unicamp.br. Adaptado.)
A figura representa a trajetória semicircular de uma molécula de massa m ionizada com carga +q e velocidade escalar V, quando penetra numa região R de um espectrômetro de massa. Nessa região atua um campo magnético uniforme perpendicular ao plano da figura, com sentido para fora dela, representado pelo símbolo $$\odot$$. A molécula atinge uma placa fotográfica, onde deixa uma marca situada a uma distância x do ponto de entrada.
Considerando as informações do enunciado e da figura, é correto afirmar que a massa da molécula é igual a
A) $$\frac{q\cdot V\cdot B\cdot x}{2}$$
B) $$\frac{2\cdot q\cdot B}{V\cdot x}$$
C) $$\frac{q\cdot B}{2\cdot V\cdot x}$$
D) $$\frac{q\cdot x}{2\cdot B\cdot V}$$
E) $$\frac{q\cdot B\cdot x}{2\cdot V}$$
3) (UNESP – 2013) A figura representa, de forma simplificada, o autódromo de Tarumã, localizado na cidade de Viamão, na Grande Porto Alegre. Em um evento comemorativo, três veículos de diferentes categorias do automobilismo, um kart (K), um fórmula 1 (F) e um stock-car (S), passam por diferentes curvas do circuito, com velocidades escalares iguais e constantes.
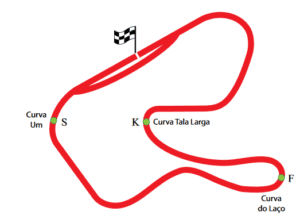
As tabelas 1 e 2 indicam, respectivamente e de forma comparativa, as massas de cada veículo e os raios de curvatura das curvas representadas na figura, nas posições onde se encontram os veículos.

Sendo $$F_{K}$$, $$F_{F}$$ e $$F_{S}$$ os módulos das forças resultantes centrípetas que atuam em cada um dos veículos nas posições em que eles se encontram na figura, é correto afirmar que
(A) $$F_{S} < F_{F} < F_{K}$$.
(B) $$F_{S} < F_{K} < F_{F}$$.
(C) $$F_{F} < F_{S} < F_{K}$$.
(D) $$F_{K} < F_{F} < F_{S}$$.
(E) $$F_{K} < F_{S} < F_{F}$$.
4) (FUVEST – 2015) A notícia “Satélite brasileiro cai na Terra após lançamento falhar”, veiculada pelo jornal O Estado de S. Paulo de 10/12/2013, relata que o satélite CBERS-3, desenvolvido em parceria entre Brasil e China, foi lançado no espaço a uma altitude de 720 km (menor do que a planejada) e com uma velocidade abaixo da necessária para colocá-lo em órbita em torno da Terra. Para que o satélite pudesse ser colocado em órbita circular na altitude de 720 km, o módulo de sua velocidade (com direção tangente à órbita) deveria ser de, aproximadamente,
a) 61 km/s
b) 25 km/s
c) 11 km/s
d) 7,7 km/s
e) 3,3 km/s
Note e adote:
raio da Terra = $$6\cdot 10^{3}\, km$$
massa da Terra = $$6\cdot 10^{24}\, kg$$
constante de gravitação universal $$G = 6,7\cdot 10^{-11}\, m^{3}/(s^{2} kg)$$
5) (UERJ – 2018) Considere a existência de um planeta homogêneo, situado em uma galáxia distante, e as informações sobre seus dois satélites apresentadas na tabela.
Sabe-se que o movimento de X e Y ocorre exclusivamente sob ação da força gravitacional do planeta. Determine a razão $$\frac{V_{X}}{V_{Y}}.
6) (UNICAMP 2017 – adaptada) Os brinquedos de parques de diversões utilizam-se de princípios da Mecânica para criar movimentos aos quais não estamos habituados, gerando novas sensações. Por isso um parque de diversões é um ótimo local para ilustrar princípios básicos da Mecânica. Um brinquedo comum em parques de diversões é o chapéu mexicano, em que cadeiras são penduradas com correntes na borda de uma estrutura circular que gira com seu eixo de rotação perpendicular ao solo. Considere um chapéu mexicano com estrutura circular de raio R = 6,3 m e correntes de comprimento L = 2 m. Ao girar, as cadeiras se elevam 40 cm, afastando-se 1,2 m do eixo de rotação, conforme mostra a figura abaixo. Calcule a velocidade angular de rotação do brinquedo.

















0 comentários