Portal da Cinemática: acesse aqui!
1) (UNICAMP – 2014) As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem substituir dezenas de trabalhadores rurais, o que pode alterar de forma significativa a relação de trabalho nas lavouras de cana-de-açúcar. A pá cortadeira da máquina ilustrada na figura abaixo gira em movimento circular uniforme a uma frequência de 300 rpm. A velocidade de um ponto extremo P da pá vale
(Considere $$\pi = 3$$)

a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
2) (UNICAMP – 2016) Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas.
Um anemômetro em que a distância entre as conchas e o centro de rotação é $$r = 25\, cm$$, em um dia cuja velocidade do vento é $$v = 18\, km/h$$, teria uma frequência de rotação de
a) 3 rpm.
b) 200 rpm.
c) 720 rpm.
d) 1200 rpm.
Se necessário, considere π ≈ 3.
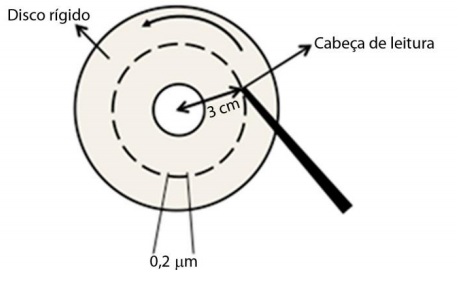
3) (UNICAMP – 2015) Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um comprimento físico de $$0,2 \mu m$$ na direção do movimento de rotação do disco. Quantas informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado apresentado abaixo? (Considere π ≈ 3.)
a) $$1,62 \cdot 10^{6}$$.
b) $$1,8 \cdot 10^{6}$$.
c) $$64,8 \cdot 10^{8}$$.
d) $$1,08 \cdot 10^{8}$$.
4) (PUCC – 2018) Para que um satélite seja utilizado para transmissões de televisão, quando em órbita, deve ter a mesma velocidade angular de rotação da Terra, de modo que se mantenha sempre sobre um mesmo ponto da superfície terrestre. Considerando R o raio da órbita do satélite, dado em km, o módulo da velocidade escalar do satélite, em km/h, em torno do centro de sua órbita, considerada circular, é
(A) $$\frac{\pi}{24} R$$.
(B) $$\frac{\pi}{12} R$$.
(C) $$\pi R$$.
(D) $$2\pi R$$.
(E) $$12\pi R$$.
5) (UNESP – 2017) Em um edifício em construção, João lança para José um objeto amarrado a uma corda inextensível e de massa desprezível, presa no ponto O da parede. O objeto é lançado perpendicularmente à parede e percorre, suspenso no ar, um arco de circunferência de diâmetro igual a 15 m, contido em um plano horizontal e em movimento uniforme, conforme a figura. O ponto O está sobre a mesma reta vertical que passa pelo ponto C, ponto médio do segmento que une João a José. O ângulo θ, formado entre a corda e o segmento de reta OC, é constante.
Considerando sen θ = 0,6, cos θ = 0,8, $$g = 10\, m/s^{2}$$ e desprezando a resistência do ar, a velocidade angular do objeto, em seu movimento de João a José, é igual a
(A) 1,0 rad/s.
(B) 1,5 rad/s.
(C) 2,5 rad/s.
(D) 2,0 rad/s.
(E) 3,0 rad/s.
6) (UNESP – 2015) A figura representa, de forma simplificada, parte de um sistema de engrenagens que tem a função de fazer girar duas hélices, $$H_{1}$$ e $$H_{2}$$. Um eixo ligado a um motor gira com velocidade angular constante e nele estão presas duas engrenagens, A e B. Esse eixo pode se movimentar horizontalmente assumindo a posição 1 ou 2. Na posição 1, a engrenagem B acopla-se à engrenagem C e, na posição 2, a engrenagem A acopla-se à engrenagem D. Com as engrenagens B e C acopladas, a hélice $$H_{1}$$ gira com velocidade angular constante $$\omega _{1}$$ e, com as engrenagens A e D acopladas, a hélice $$H_{2}$$ gira com velocidade angular constante $$\omega _{2}$$.
Considere $$r_{A}$$, $$r_{B}$$, $$r_{C}$$ e $$r_{D}$$ os raios das engrenagens A, B, C e D, respectivamente. Sabendo que $$r_{B} = 2\cdot r_{A}$$ e que $$r_{C} = r_{D}$$, é correto afirmar que a relação $$\frac{\omega _{1}}{\omega _{2}}$$ é igual a
(A) 1,0.
(B) 0,2.
(C) 0,5.
(D) 2,0.
(E) 2,2.
7) (UEMG – 2018) Em uma viagem a Júpiter, deseja-se construir uma nave espacial com uma seção rotacional para simular, por efeitos centrífugos, a gravidade. A seção terá um raio de 90 metros. Quantas rotações por minuto (RPM) deverá ter essa seção para simular a gravidade terrestre? (considere g = 10 m/s²).
(A) 10/π
(B) 2/π
(C) 20/π
(D) 15/π
8) (FUVEST – 2017 – adaptada) De férias em Macapá, cidade brasileira situada na linha do equador e a 51° de longitude oeste, Maria faz um selfie em frente ao monumento do marco zero do equador. Ela envia a foto a seu namorado, que trabalha em um navio ancorado próximo à costa da Groenlândia, a 60° de latitude norte e no mesmo meridiano em que ela está. Considerando apenas os efeitos da rotação da Terra em torno de seu eixo, determine, para essa situação, o módulo $$a_{M}$$ da aceleração de Maria e a medida do ângulo entre as direções das acelerações de Maria e de seu namorado.
Note e adote:
Maria e seu namorado estão parados em relação à superfície da Terra.
As velocidades e acelerações devem ser determinadas em relação ao centro da Terra.
Considere a Terra uma esfera com raio $$6\cdot 10^{6}\, m$$.
Duração do dia ≈ 80.000 s
π ≈ 3
Ignore os efeitos da translação da Terra em torno do Sol.
sen 30° = cos 60° = 0,5
sen 60° = cos 30° ≈ 0,9
9) (UNESP – 2017/2) As pás de um gerador eólico de pequeno porte realizam 300 rotações por minuto. A transformação da energia cinética das pás em energia elétrica pelo gerador tem rendimento de 60%, o que resulta na obtenção de 1 500 W de potência elétrica.
Considerando π = 3, calcule o módulo da velocidade angular, em rad/s, e da velocidade escalar, em m/s, de um ponto P situado na extremidade de uma das pás, a 1,2 m do centro de rotação. Determine a quantidade de energia cinética, em joules, transferida do vento para as pás do gerador em um minuto. Apresente os cálculos.
10) (UNICAMP – 2017) Os brinquedos de parques de diversões utilizam-se de princípios da Mecânica para criar movimentos aos quais não estamos habituados, gerando novas sensações. Por isso um parque de diversões é um ótimo local para ilustrar princípios básicos da Mecânica.
a) Considere uma montanha russa em que um carrinho desce por uma rampa de altura H=5m e, ao final da rampa, passa por um trecho circular de raio R=2m, conforme mostra a figura a) abaixo. Calcule o módulo da aceleração no ponto mais baixo do circuito, considerando que o carrinho partiu do repouso.
b) Outro brinquedo comum em parques de diversões é o chapéu mexicano, em que cadeiras são penduradas com correntes na borda de uma estrutura circular que gira com seu eixo de rotação perpendicular ao solo. Considere um chapéu mexicano com estrutura circular de raio R = 6,3 m e correntes de comprimento L = 2 m. Ao girar, as cadeiras se elevam 40 cm, afastando-se 1,2 m do eixo de rotação, conforme mostra a figura b) abaixo. Calcule a velocidade angular de rotação do brinquedo.
11) (UNICAMP – 2022 – adaptada) O órgão Hammond, instrumento eletromecânico inventado por Laurens Hammond e John Hanert em 1935, como alternativa aos órgãos de tubos em igrejas, rapidamente tornou-se popular entre músicos de jazz e de outros gêneros musicais. O funcionamento do instrumento é baseado num conjunto de rodas fônicas (discos metálicos com dentes magnetizados) que giram próximas a bobinas eletromagnéticas (sensores), conforme a figura A. À medida que os dentes passam em frente ao sensor, o fluxo magnético através da bobina varia, dando origem a uma corrente elétrica que oscila com um período correspondente à passagem de cada dente. Essa corrente elétrica é então amplificada e alimenta os alto-falantes. Se a roda fônica da nota Lá, de frequência f = 220 Hz, possui 8 dentes e tem um raio R = 3,0 cm, qual é o módulo da velocidade linear de um ponto na extremidade de um dente?
12) Um móvel parte do repouso e percorre uma circunferência de raio de 20cm em MCUV. Após 2s, percorreu 5 voltas. Determine:
a) a aceleração angular
b) a aceleração linear
c) a velocidade linear ao final de 5 voltas
d) o tempo necessário para percorrer 20 voltas
13) Um móvel em trajetória circular de raio r = 5m parte do repouso com aceleração angular constante de $$10rad/s^{2}$$. Quantas voltas ele percorre nos 10 primeiros segundos ?
14) Um “motorzinho” de dentista gira com frequência de 2000 Hz até a broca de raio 2,0 mm encostar no dente do paciente, quando, após 1,5 s, passa a ter frequência de 500 Hz. Determine o módulo da aceleração escalar média e a aceleração angular média neste intervalo de tempo.

















0 comentários