Portal da Energia: acesse aqui!
1) (UERJ 2019) Uma composição do metrô, com 400 passageiros em cada vagão, desloca-se com velocidade de 36 km/h. Nessas condições, determine, em joules, a energia cinética total da composição.
2) (FATEC – 2016) Desprezando-se a massa do motorista, assinale a alternativa que apresenta, em joules, a variação da energia cinética desse automóvel, do início da frenagem até o momento de sua parada.
(A) $$+ 4,0\cdot 10^{5}$$
(B) $$+ 3,0\cdot 10^{5}$$
(C) $$+ 0,5\cdot 10^{5}$$
(D) $$- 4,0\cdot 10^{5}$$
(E) $$- 2,0\cdot 10^{5}$$
Lembre-se de que: $$E_{C} = \frac{m\cdot v^{2}}{2}$$, em que $$E_{C}$$ é dada em joules, m em quilogramas e v em metros por segundo.
3) (UNICAMP – 2016 – ADAPTADA) Recentemente, a sonda New Horizons tornou-se a primeira espaçonave a sobrevoar Plutão, proporcionando imagens espetaculares desse astro distante. A sonda New Horizons foi lançada da Terra pelo veículo espacial Atlas V 511, a partir do Cabo Canaveral. O veículo, com massa total $$m = 6\cdot 10^{5}\, kg$$, foi o objeto mais rápido a ser lançado da Terra para o espaço até o momento. O trabalho realizado pela força resultante para levá-lo do repouso à sua velocidade máxima foi de $$\tau = 768\cdot 10^{11}\, J$$. Considerando que a massa total do veículo não variou durante o lançamento, calcule sua velocidade máxima.
4) (FUVEST – 2017 – ADAPTADA) Um atleta de peso 700 N corre 100 metros rasos em 10 segundos. Os gráficos dos módulos da sua velocidade horizontal, v, e da sua aceleração horizontal, a, ambas em função do tempo t, estão na página de respostas. Determine a energia cinética E do atleta no instante t = 10s;
Note e adote: Aceleração da gravidade = $$10 m/s^{2}$$
5) (UERJ – 2017) Duas carretas idênticas, A e B, trafegam com velocidade de 50 km/h e 70 km/h, respectivamente. Admita que as massas dos motoristas e dos combustíveis são desprezíveis e que $$E_{A}$$ é a energia cinética da carreta A e $$E_{B}$$ a da carreta B. A razão $$\frac{E_{A}}{E_{B}}$$ equivale a:
(A) $$\frac{5}{7}$$
(B) $$\frac{8}{14}$$
(C) $$\frac{25}{49}$$
(D) $$\frac{30}{28}$$
6) (UNESP – 2013) Em um jogo de sinuca, a bola A é lançada com velocidade $$\vec{V}$$ de módulo constante e igual a 2 m/s em uma direção paralela às tabelas (laterais) maiores da mesa, conforme representado na figura 1. Ela choca-se de forma perfeitamente elástica com a bola B, inicialmente em repouso, e, após a colisão, elas se movem em direções distintas, conforme a figura 2.
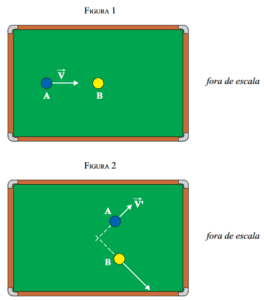
Sabe-se que as duas bolas são de mesmo material e idênticas em massa e volume. A bola A tem, imediatamente depois da colisão, velocidade $$\vec{V’}$$ de módulo igual a 1 m/s. Desprezando os atritos e sendo $$Eꞌ_{B}$$ a energia cinética da bola B imediatamente depois da colisão e $$E_{A}$$ a energia cinética da bola A antes da colisão, a razão $$\frac{E’_{B}}{E_{A}}$$ é igual a
(A) $$\frac{3}{4}$$
(B) $$\frac{1}{2}$$
(C) $$\frac{4}{5}$$
(D) $$\frac{2}{3}$$
(E) $$\frac{1}{5}$$
7) (UNICAMP – 2013) Um aerogerador, que converte energia eólica em elétrica, tem uma hélice como a representada na figura abaixo. A massa do sistema que gira é M = 50 toneladas, e a distância do eixo ao ponto P, chamada de raio de giração, é R = 10 m. A energia cinética do gerador com a hélice em movimento é dada por $$\frac{1}{2}\cdot M\cdot V_{P} ^{2}$$, sendo $$V_{P}$$ o módulo da velocidade do ponto P. Se o período de rotação da hélice é igual a 2 s, qual é a energia cinética do gerador? Considere $$\pi = 3$$.
a) $$6,250\cdot 10^{5}\, J$$
b) $$2,250\cdot 10^{7}\, J$$.
c) $$5,625\cdot 10^{7}\, J$$.
d) $$9,000\cdot 10^{7}\, J$$.
8) (UERJ 2019) O vagão de uma composição do metrô possui 12 lâmpadas eletrônicas idênticas, de 25 W cada uma. Essas lâmpadas ficam acesas durante 15 horas em cada dia. Admita que a tarifa praticada pela concessionária de energia elétrica seja igual a R$ 0,80 por kWh consumido. Calcule, em reais, o valor do consumo de energia elétrica das lâmpadas do vagão em um período de 30 dias.
9) (FUVEST – 2017 – ADAPTADA) A determinação da massa da molécula de insulina é parte do estudo de sua estrutura. Para medir essa massa, as moléculas de insulina são previamente ionizadas, adquirindo, cada molécula, a carga de um elétron. Esses íons (I) são liberados com velocidade inicial nula a partir de uma amostra submetida a um potencial V = – 20 kV. Os íons são acelerados devido à diferença de potencial entre a amostra e um tubo metálico, em potencial nulo, no qual passam a se mover com velocidade constante. Para a calibração da medida, adiciona-se à amostra um material padrão cujas moléculas também são ioniza das, adquirindo, cada uma, a carga de um elétron; esses íons (P) têm massa conhecida igual a 2846 u. A situação está esquematizada na figura.
Determine a energia cinética E dos íons, quando estão dentro do tubo. O gráfico na página de respostas mostra o número N de íons em função do tempo t despendido para percorrerem o comprimento L do tubo. Determine a razão $$R_{m} = \frac{m_{I}}{m_{P}}$$ entre as massas $$m_{I}$$ e $$m_{P}$$, respectivamente, de um íon de insulina e de um íon P.
Note e adote: A amostra e o tubo estão em vácuo. u = unidade de massa atômica. Carga do elétron: $$e = -1,6\cdot 10^{-19}\, C.$$ $$1 \mu s = 10^{-6}\, s.$$
10) (UNESP – 2017) Observe o poema visual de E. M. de Melo e Castro.
Suponha que o poema representa as posições de um pêndulo simples em movimento, dadas pelas sequências de letras iguais. Na linha em que está escrita a palavra pêndulo, indicada pelo traço vermelho, cada letra corresponde a uma localização da massa do pêndulo durante a oscilação, e a letra P indica a posição mais baixa do movimento, tomada como ponto de referência da energia potencial. Considerando as letras da linha da palavra pêndulo, é correto afirmar que
(A) a energia cinética do pêndulo é máxima em P.
(B) a energia potencial do pêndulo é maior em Ê que em D.
(C) a energia cinética do pêndulo é maior em L que em N.
(D) a energia cinética do pêndulo é máxima em O.
(E) a energia potencial do pêndulo é máxima em P.
11) (FUVEST – 2015) A figura abaixo mostra o gráfico da energia potencial gravitacional U de uma esfera em uma pista, em função da componente horizontal x da posição da esfera na pista.
A esfera é colocada em repouso na pista, na posição de abscissa $$x=x_{1}$$, tendo energia mecânica E<0. A partir dessa condição, sua energia cinética tem valor
a) máximo igual a |$$U_{0}$$|.
b) igual a |E| quando $$x=x_{3}$$.
c) mínimo quando $$x=x_{2}$$.
d) máximo quando $$x=x_{3}$$.
e) máximo quando $$x=x_{2}$$.
Note e adote: desconsidere efeitos dissipativos.
12) (UNESP – 2017) As pás de um gerador eólico de pequeno porte realizam 300 rotações por minuto. A transformação da energia cinética das pás em energia elétrica pelo gerador tem rendimento de 60%, o que resulta na obtenção de 1 500 W de potência elétrica.
Considerando π = 3, calcule o módulo da velocidade angular, em rad/s, e da velocidade escalar, em m/s, de um ponto P situado na extremidade de uma das pás, a 1,2 m do centro de rotação. Determine a quantidade de energia cinética, em joules, transferida do vento para as pás do gerador em um minuto. Apresente os cálculos.
13) (UNICAMP 2008 – ADAPTADA) Um experimento interessante pode ser realizado abandonando-se de certa altura uma bola de basquete com uma bola de pingue-pongue (tênis de mesa) em repouso sobre ela, conforme mostra a figura (a). Após o choque da bola de basquete com o solo, e em seguida com a bola de pingue-pongue, esta última atinge uma altura muito maior do que sua altura inicial.
a) Para h = 80 cm, calcule a velocidade com que a bola de basquete atinge o solo. Despreze a resistência do ar.
14) (UNICAMP – 2017 – ADAPTADA) A energia solar é a única fonte de energia do avião Solar Impulse 2, desenvolvido na École Polytechnique Fédérale de Lausanne, Suíça. Para aproveitar a energia obtida dos raios solares e poder voar tanto à noite quanto de dia, o Solar Impulse 2, de massa aproximada m=2000kg, voava em alta altitude e velocidade $$v_{dia}=90\, km/h$$ durante o dia, armazenando energia solar para a noite. Ao anoitecer, o avião descia para altitudes menores e voava a uma velocidade aproximada de $$v_{noite}=57,6\, km/h$$. Qual é a variação da energia cinética do avião entre o dia e a noite?
15) (UNESP – 2016) Ótimos nadadores, os golfinhos conseguem saltar até 5 m acima do nível da água do mar. Considere que um golfinho de 100 kg, inicialmente em repouso no ponto A, situado 3 m abaixo da linha da água do mar, acione suas nadadeiras e atinja, no ponto B, determinada velocidade, quando inicia o seu movimento ascendente e seu centro de massa descreve a trajetória indicada na figura pela linha tracejada. Ao sair da água, seu centro de massa alcança o ponto C, a uma altura de 5 m acima da linha da água, com módulo da velocidade igual a $$4\sqrt{10}\, m/s$$, conforme a figura.
Considere que, no trajeto de B para C, o golfinho perdeu 20% da energia cinética que tinha ao chegar no ponto B, devido à resistência imposta pela água ao seu movimento. Desprezando a resistência do ar sobre o golfinho fora da água, a velocidade da água do mar e adotando $$g = 10 m/s^{2}$$, é correto afirmar que o módulo da quantidade de movimento adquirida pelo golfinho no ponto B, em $$kg\cdot m/s$$, é igual a
(A) 1 800.
(B) 2 000.
(C) 1 600.
(D) 1 000.
(E) 800.
16) (UNICAMP – 2017 – ADAPTADA) Os brinquedos de parques de diversões utilizam-se de princípios da Mecânica para criar movimentos aos quais não estamos habituados, gerando novas sensações. Por isso um parque de diversões é um ótimo local para ilustrar princípios básicos da Mecânica. Considere uma montanha russa em que um carrinho desce por uma rampa de altura H=5m e, ao final da rampa, passa por um trecho circular de raio R=2m, conforme mostra a figura abaixo. Calcule o módulo da aceleração no ponto mais baixo do circuito, considerando que o carrinho partiu do repouso.
17) (PUCC – 2017) Na formação escolar é comum tratarmos de problemas ideais, como lançamentos verticais de objetos nos quais se despreza a resistência do ar. Mas podemos também abordar um problema destes sem esta simplificação. Um objeto é lançado verticalmente pra cima, a partir do solo, com velocidade 20 m/s. Na subida este objeto sofre uma perda de 15% em sua energia mecânica devido às forças dissipativas. Adotando-se $$g = 10\, m/s^{2}$$, a altura máxima que será atingida por este objeto em relação ao solo será, em metros, de:
(A) 17.
(B) 10.
(C) 25.
(D) 8.
(E) 150.
18) (FGV – 2018) A força de atrito no trecho BC permaneceu constante, e o coeficiente de atrito entre os pneus e o pavimento no trecho BC era de
(A) 0,20.
(B) 0,25.
(C) 0,28.
(D) 0,36.
(E) 0,40.
19) (FGV – 2018) A velocidade com que o automóvel passou pelo ponto A, em km/h, e a intensidade da força resultante sobre ele, em função de M, nesse percurso AB, foram, correta e respectivamente,
(A) 36 e 1,00M.
(B) 72 e 1,00M.
(C) 72 e 1,25M.
(D) 90 e 1,25M.
(E) 90 e 1,50M.
20) (FGV – 2018) A energia mecânica dissipada na colisão, em função de M, foi
(A) 160M.
(B) 145M.
(C) 142,5M.
(D) 137,5M.
(E) 125M.
21) A equação horária da velocidade de um móvel de 20 quilogramas é dada por: v = 3 + 0,2 t, em unidades do SI. Podemos afirmar que a energia cinética desse móvel, no instante t = 10 s, vale:
a) 45 J
b) 100 J
c) 200 J
d) 250 J
e) 2.000 J
22) (VUNESP – 2002) Uma pedra é lançada por um garoto seguindo uma direção que forma ângulo de 60° com a horizontal e com energia cinética inicial E. Sabendo que cos 60° = 1/2 e supondo que a pedra esteja sujeita exclusivamente à ação da gravidade, o valor de sua energia cinética no ponto mais alto da trajetória vale:
a) zero
b) E/4
c) E/2
d) 3 E/4
e) E
23) (UNESP – 2017)Um garoto arremessa uma bola com velocidade inicial inclinada de um ângulo α com a horizontal. A bola abandona a mão do garoto com energia cinética $$E_{0}$$ e percorre uma trajetória parabólica contida em um plano vertical, representada parcialmente na figura.
Desprezando-se a resistência do ar, a energia cinética da bola no ponto mais alto de sua trajetória é
(A)$$E_{0}\cdot sen\,\alpha$$
(B)$$E_{0}\cdot cos\,\alpha$$
(C)$$E_{0}\cdot cos^{2}\,\alpha$$
(D)$$E_{0}\cdot sen^{2}\,\alpha$$
(E)$$\frac{E_{0}\cdot sen^{2}\,\alpha}{2}$$
24) (ENEM – 2015) Um carro solar é um veículo que utiliza apenas a energia solar para a sua locomoção. Tipicamente, o carro contém um painel fotovoltaico que converte a energia do Sol em energia elétrica que, por sua vez, alimenta um motor elétrico. A imagem mostra o carro solar Tokai Challenger, desenvolvido na Universidade de Tokai, no Japão, e que venceu o World Solar Challenge de 2009, uma corrida internacional de carros solares, tendo atingido uma velocidade média acima de 100 km/h.
Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área que chega à superfície da Terra) seja de $$1.000\, W/m^{2}$$, que o carro solar possua massa de 200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de $$9,0\, m^{2}$$ e rendimento de 30%. Desprezando as forças de resistência do ar, o tempo que esse carro solar levaria, a partir do repouso, para atingir a velocidade de 108 km/h é um valor mais próximo de
A) 1,0 s.
B) 4,0 s.
C) 10 s.
D) 33 s.
E) 300 s.
25) (UNICAMP – 2022) A viagem desde o Columbia até a superfície da Lua foi realizada no Módulo Lunar Eagle, formado por dois estágios: um usado na descida e outro, na subida. A massa seca do estágio de subida, ou seja, sem contar a massa do combustível (quase totalmente consumido na viagem de volta), era m ≅ 2500 kg. Considere que o módulo da aceleração gravitacional seja aproximadamente constante e dado por $$g\cong g_{orb} = 1,4\, m/s^{2}$$ desde a superfície lunar até a órbita do Columbia, que se situava a uma altitude h = 110 km. Qual é a variação da energia potencial gravitacional do estágio de subida (massa seca que reencontra o Columbia) na viagem de volta?
a) $$3,85\times 10^{5}\, J$$.
b) $$2,85\times 10^{8}\, J$$.
c) $$3,85\times 10^{8}\, J$$.
d) $$2,75\times 10^{9}\, J$$.
26) (PUCCAMP – 2022) Atenção: Para responder às questões de números 28 a 30, considere o texto abaixo.
Aquecimento do Oceano
Os oceanos do planeta Terra absorveram uma quantidade recorde de calor no ano passado, de acordo com um novo estudo, que analisou dados de 1950 a 2019. Segundo as informações, a temperatura média dos oceanos em 2019 era 0,075°C, acima da média de 1981 a 2010. Pode parecer pouco, mas, considerando o grande volume dos oceanos, até mesmo um pequeno aumento exigiria um fluxo impressionante de calor – o equivalente a 228 sextilhões de Joules, segundo o estudo de uma equipe internacional de cientistas, publicado na revista Advances in Atmospheric Sciences. A pesquisa do grupo fornece evidências incontestáveis de que o planeta está esquentando – e rapidamente. De 1987 a 2019, os oceanos esquentaram quatro vezes e meia mais rapidamente do que entre 1955 e 1986. Quando os oceanos esquentam, o gelo derrete mais rápido e a água se expande, ocupando mais espaço e fazendo o nível do mar subir. Além disso, oceanos mais quentes significam mais água evaporando na atmosfera, criando mais umidade, o que pode sobrecarregar as tempestades. (Disponível em: https://olhardigital.com.br)
Considere que a massa da Terra seja igual a $$6,0\times 10^{24}\, kg$$ e que sua velocidade média de translação ao redor do Sol seja 30 km/s. A energia cinética da Terra nesse movimento é maior do que a quantidade de calor responsável pelo aumento da temperatura dos oceanos nos últimos anos ($$2,28\times 10^{23}\, J$$) de um fator aproximadamente igual a:
(A) $$10^{6}$$
(B) $$10^{10}$$
(C) $$10^{15}$$
(D) $$10^{18}$$
(E) $$10^{23}$$
27) (UNESP – 2022) Uma pequena esfera é abandonada do repouso no ponto 1 e, após deslizar sem rolar pela pista mostrada em corte na figura, perde contato com ela no ponto 2, passando a se mover em trajetória parabólica, até atingir o solo horizontal.
Adotando g = 10 m/s², desprezando o atrito e a resistência do ar, quando a esfera passar pelo ponto 3, ponto mais alto de sua trajetória fora da pista, a componente horizontal da velocidade vetorial da esfera terá módulo igual a
(A) 1,0 m/s.
(B) 1,8 m/s.
(C) 2,0 m/s.
(D) 1,5 m/s.
(E) 2,5 m/s.
28) (UNICAMP – 2022 – adaptada) Recentemente, cientistas internacionais realizaram um estudo sobre as opções para evitar um possível impacto de um asteroide com a Terra e estimaram que o tempo mínimo de antecedência do início das ações para impedir a colisão é de cinco anos. Considere um asteroide de massa $$M = 3,0\times 10^{15}\, kg$$ (comparável com a massa do asteroide que supostamente colidiu com a Terra e causou a extinção dos dinossauros) se deslocando em direção à Terra com uma quantidade de movimento de módulo $$|\vec{Q}_{i}| = 1,2\times 10^{20}\, N\cdot s$$. Na tentativa de evitar o impacto, pretende-se lançar um míssil da Terra em direção ao asteroide de modo que, com o choque, seja gerado um impulso que altere a velocidade do asteroide (em módulo ou direção). Suponha que essa operação ocorra com sucesso, reduzindo o módulo da velocidade de deslocamento do asteroide pela metade. Desprezando a variação da massa do asteroide durante a operação, calcule a variação da energia cinética do asteroide como resultado da operação.
29) (UNICAMP – 2022 – adaptada) Uma nova forma de geração de energia elétrica eólica que vem sendo testada usa a vibração de uma haste vertical de carbono produzida pela força do vento. A energia da oscilação da haste é transformada em energia elétrica por meio de alternadores. Esse sistema apresenta vantagens para o meio ambiente, uma vez que não utiliza as turbinas eólicas convencionais por serem muito barulhentas e perturbarem as comunidades vizinhas e a migração de pássaros. O movimento da extremidade superior da haste do item (a) é similar ao de um pêndulo. Um pêndulo simples, de comprimento L = 2,0 m e massa m em sua extremidade inferior (a massa da haste em si é desprezível), é solto a partir do repouso do ângulo $$\theta_{0} = 26^{\circ}$$ (veja a figura B). Despreze perdas por atrito e calcule a velocidade da massa m quando ela passa pelo ponto mais baixo da trajetória. Dados: sen 26°≅0,44, cos 26°≅0,9, tan 26°≅0,49.
30) (FUVEST – 2022 – adaptada) Uma bola de borracha de massa 𝑚 = 50 gramas é abandonada do repouso, a partir de uma certa altura ℎ. A resistência do ar não é desprezível, e o movimento da bola durante 0,6 segundo após o início da queda é registrado por uma câmera de alta resolução. Considerando o esquema da situação inicial e os gráficos da dependência temporal da altura 𝑦 e da velocidade vertical $$v_{y}$$ da bola, responda às questões a seguir.
Calcule a energia cinética perdida pela bola entre os instantes imediatamente antes e imediatamente depois do choque com o solo e o módulo da força média de resistência do ar atuando sobre a bola entre o instante inicial e o instante imediatamente antes de ela atingir o solo pela primeira vez.
31) (UERJ – 2019) Um bloco de massa m desliza sem atrito sobre uma superfície, passando sucessivamente pelos pontos A, B, C e D, conforme indicado no esquema.
Sendo $$E_{MA}$$, $$E_{MB}$$, $$E_{MC}$$ e $$E_{MD}$$, respectivamente, a energia mecânica nos pontos A, B, C e D, a relação entre elas é:
(A) $$E_{MA} > E_{MC} < E_{MB} = E_{MD}$$
(B) $$E_{MA} > E_{MB} > E_{MC} < E_{MD}$$
(C) $$E_{MA} < E_{MB} < E_{MC} > E_{MD}$$
(D) $$E_{MA} = E_{MB} = E_{MC} = E_{MD}$$
32) (UNICAMP – 2014) Andar de bondinho no complexo do Pão de Açúcar no Rio de Janeiro é um dos passeios aéreos urbanos mais famosos do mundo. Marca registrada da cidade, o Morro do Pão de Açúcar é constituído de um único bloco de granito, despido de vegetação em sua quase totalidade e tem mais de 600 milhões de anos.
A altura do Morro da Urca é de 220 m e a altura do Pão de Açúcar é de cerca de 400 m, ambas em relação ao solo. A variação da energia potencial gravitacional do bondinho com passageiros de massa total M = 5000 kg, no segundo trecho do passeio, é (Use $$g = 10 m/s^{2}$$.)
a) $$11\cdot 10^{6}\, J$$.
b) $$20\cdot 10^{6}\, J$$.
c) $$31\cdot 10^{6}\, J$$.
d) $$9\cdot 10^{6}\, J$$.
33) Uma pessoa, com 80 kg de massa, gasta para realizar determinada atividade física a mesma quantidade de energia que gastaria se subisse diversos degraus de uma escada, equivalente a uma distância de 450 m na vertical, com velocidade constante, num local onde g = 10 m/s². A tabela a seguir mostra a quantidade de energia, em joules, contida em porções de massas iguais de alguns alimentos.
Considerando que o rendimento mecânico do corpo humano seja da ordem de 25%, ou seja, que um quarto da energia química ingerida na forma de alimentos seja utilizada para realizar um trabalho mecânico externo por meio da contração e expansão de músculos, para repor exatamente a quantidade de energia gasta por essa pessoa em sua atividade física, ela deverá ingerir 4 porções de
(A) castanha de caju.
(B) batata frita.
(C) chocolate.
(D) pizza de mussarela.
(E) espaguete.

















0 comentários