Lista de exercícios com gabarito e resolução sobre Função Afim (função do 1º Grau). Questões de fixação, vestibulares e ENEM.
O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total, em reais, das vendas que ele efetuar durante o mês. Em um mês em que suas vendas totalizarem x reais, o salário do vendedor será dado pela expressão:
A) 750 + 2,5x
B) 750 + 0,25x
C) 750,25x
D) 750(0,25x)
E) 750 + 0,025x
Solução (clique aqui)
(UNESP) O gráfico representa a vazão resultante de água, em m³/h, em um tanque, em função do tempo, em horas. Vazões negativas significam que o volume de água no tanque está diminuindo.
São feitas as seguintes afirmações:
I.No intervalo de A até B, o volume de água no tanque é constante.
II.No intervalo de B até E, o volume de água no tanque está crescendo.
III.No intervalo de E até H, o volume de água no tanque está decrescendo.
IV.No intervalo de C até D, o volume de água no tanque está crescendo mais rapidamente.
V.No intervalo de F até G, o volume de água no tanque está decrescendo mais rapidamente.
É correto o que se afirma em:
(A) I, III e V, apenas.
(B) II e IV, apenas.
(C) I, II e III, apenas.
(D) III, IV e V, apenas.
(E) I, II, III, IV e V.
Gabarito: e)
Solução (clique aqui)
(UNICAMP) O gráfico abaixo exibe o lucro líquido (em milhares de reais) de três pequenas empresas A, B e C, nos anos de 2013 e 2014.
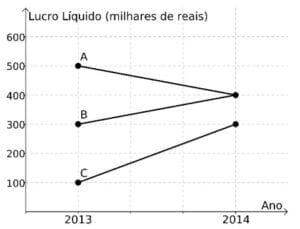
Com relação ao lucro líquido, podemos afirmar que
a) A teve um crescimento maior do que C.
b) C teve um crescimento maior do que B.
c) B teve um crescimento igual a A.
d) C teve um crescimento menor do que B.
Solução: (clique aqui)
(ENEM) Em fevereiro, o governo da Cidade do México, metrópole com uma das maiores frotas de automóveis do mundo, passou a oferecer à população bicicletas como opção de transporte. Por uma anuidade de 24 dólares, os usuários têm direito a 30 minutos de uso livre por dia. O ciclista pode retirar em uma estação e devolver em qualquer outra e, se quiser estender a pedalada, paga 3 dólares por hora extra.
A expressão que relaciona o valor f pago pela utilização da bicicleta por um ano, quando se utilizam x horas extras nesse período é
a) f(x) = 3x
b) f(x) = 24
c) f(x) = 27
d) f(x) = 3x + 24
e) f(x) = 24x + 3
Solução (clique aqui)
(PUC- Campinas) Para produzir um número n de peças (n inteiro positivo), uma empresa deve investir R$ 200.000,00 em máquinas e, além disso, gastar R$0,50 na produção de cada peça. Nessas condições, o custo C, em reais, da produção de n peças é uma função de n dada por
a) C(n) = 200 000 + 0,50
b) C(n) = 200 000n
c) C(n) = n/2 + 200 000
d) C(n) = 200 000 – 0,50n
e) C(n) = (200 000 + n)/2
Solução (clique aqui)
(FGV) Sejam f e g funções de R em R definidas por f(x) = kx + 3 e g (x) = 2x. Se f(g(–3)) = – 9, então a função gof é dada por:
a) g(f(x)) = 4x + 3
b) g(f(x)) = 4x – 3
c) g(f(x)) = 4x + 9
d) g(f(x)) = 4x – 6
e) g(f(x)) = 4x + 6
Solução (clique aqui)
(PUC – MG) A função linear R(t) = at + b expressa o rendimento R, em milhares de reais, de certa aplicação. O tempo t é contado em meses, R(1) = –1 e R(2) = 1. Nessas condições, o rendimento obtido nessa aplicação, em quatro meses, é… Solução
(ENEM) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.
A representação algébrica do lucro (L) em função do tempo (t) é
a) L(t) = 20t + 3000
b) L(t) = 20t + 4000
c) L(t) = 200t
d) L(t) = 200t – 1000
e) L(t) = 200t + 3000
Solução: (clique aqui)
(ENEM 2020) Por muitos anos, o Brasil tem figurado no cenário mundial entre os maiores produtores e exportadores de soja. Entre os anos de 2010 e 2014, houve uma forte tendência de aumento da produtividade, porém, um aspecto dificultou esse avanço: o alto custo do imposto ao produtor associado ao baixo preço de venda do produto.
Em média, um produtor gastava R$ 1200,00 por hectare plantado, e vendia por R$ 50,00 cada saca de 60 kg. Ciente desses valores, um produtor pode, em certo ano, determinar uma relação do lucro L que obteve em função das sacas de 60 kg vendidas. Suponha que ele plantou 10 hectares de soja em sua propriedade, na qual colheu x sacas de 60 kg e todas as sacas foram vendidas.
Disponível em: www.cnpso.embrapa.br. Acesso em: 27 fev. 2012 (adaptado).
Qual é a expressão que determinou o lucro L em função de x obtido por esse produtor nesse ano?
a)L(x) = 50x – 1 200
b)L(x) = 50x – 12 000
c)L(x) = 50x + 12 000
d)L(x) = 500x – 1 200
e)L(x) = 1 200x – 500
(FGV) Uma fábrica de panelas opera com um custo fixo mensal de R$ 9.800,00 e um custo variável por panela de R$ 45,00. Cada panela é vendida por R$ 65,00. Seja x a quantidade que deve ser produzida e vendida mensalmente para que o lucro mensal seja igual a 20%
da receita. A soma dos algarismos de x é… Solução
(Cesgranrio) O valor de um carro novo é de R$ 9 000,00 e, com 4 anos de uso, é de R$ 4 000,00. Supondo que o preço caia com o tempo, segundo uma linha reta, o valor de um carro com 1 ano de uso é
A) R$ 8 250,00.
B) R$ 8 000,00.
C) R$ 7 750,00.
D) R$ 7 500,00.
E) R$ 7 000,00.
(ENEM) Uma fatura mensal de água é composta por uma taxa fixa, independentemente do gasto, mais uma parte relativa ao consumo de água, em metro cúbico. O gráfico relaciona o valor da fatura com o volume de água gasto em uma residência no mês de novembro, representando uma semirreta.
Observa-se que, nesse mês, houve um consumo de 7 m³ de água. Sabe-se que, em dezembro, o consumo de água nessa residência, em metro cúbico, dobrou em relação ao mês anterior. O valor da fatura referente ao consumo no mês de dezembro nessa residência foi
superior a R$ 65,00 e inferior a R$ 70,00.
superior a R$ 80,00 e inferior a R$ 85,00.
superior a R$ 90,00 e inferior a R$ 95,00.
superior a R$ 95,00.
inferior a R$ 55,00.
(UERJ) Sabe-se que, nos pulmões, o ar atinge a temperatura do corpo e que, ao ser exalado, tem temperatura inferior à do corpo, já que é resfriado nas paredes do nariz. Através de medições realizadas em um laboratório foi obtida a função:
$$T_{A} = 8,5 + 0,75\cdot T_{B}$$, 12° ≤ $$T_{B}$$ ≤ 30°,
em que $$T_{A}$$ e $$T_{B}$$ representam, respectivamente, a temperatura do ar exalado e a do ambiente.
Calcule:
a) a temperatura do ambiente quando $$T_{A}= 25 °C$$;
b) o maior valor que pode ser obtido para $$T_{A}$$.
(ENEM) As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18 bilhões de sacolas plásticas. Os supermercados brasileiros se preparam para acabar com as sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o ano de 2007.
De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidos em 2011?
A) 4,0
B) 6,5
C) 7,0
D) 8,0
E) 10,0
(Cesgranrio) Uma barra de ferro com temperatura inicial de –10 °C foi aquecida até 30 °C. O gráfico a seguir representa a variação da temperatura da barra em função do tempo gasto nessa experiência. Calcule em quanto tempo, após o início da experiência, a temperatura da barra atingiu 0 °C.
a) 1 min
b) 1min e 5s
c) 1min e 10s
d) 1min e 15s
e) 1min e 20s
(ENEM 2018/ppl) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).
A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é
a)-$$10x+500$$
b)-$$x/10+50$$
c)$$-x/10+500$$
d)$$x/10+50$$
e)$$x/10+500$$
Solução (clique aqui)
(EspCEx) Considere as funções reais f(x) = 3x, de domínio [4, 8], e g(y) = 4y, de domínio [6, 9]. Os valores máximo e mínimo que o quociente $$\frac{f(x)}{g(y)}$$ pode assumir são, respectivamente:
a) 2/3 e 1/2
b) 1/3 e 1
c) 4/3 e 3/4
d) 3/4 e 1/3
e) 1 e 1/3
Solução (clique aqui)
(ENEM) O percentual da população brasileira conectada à internet aumentou nos anos de 2007 a 2011. Conforme dados do Grupo Ipsos, essa tendência de crescimento é mostrada no gráfico.
Suponha que foi mantida, para os anos seguintes, a mesma taxa de crescimento registrada no período 2007-2011.
A estimativa para o percentual de brasileiros conectados à internet em 2013 era igual a
a) 56,40%.
b) 58,50%.
c) 60,60%.
d) 63,75%.
e) 72,00%.
Solução: (clique aqui)
(UERJ) Os veículos para transporte de passageiros em determinado município têm vida útil que varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos está representada a desvalorização
de quatro desses veículos ao longo dos anos, a partir de sua compra na fábrica.
Com base nos gráficos, o veículo que mais desvalorizou por ano foi:
a) I
b) II
c) III
d) IV
Solução: (clique aqui)
(PUC – MG) Uma função do 1º grau é tal que f(–1) = 5 e f(3)= –3. Então, f(0) é igual a
a) 0
b) 2
c) 3
d) 4
e) -1
Solução (clique aqui)
(FGV) Uma fábrica de paletós trabalha com um custo fixo mensal de R$ 10.000,00 e um custo variável de R$ 100,00 por paletó. O máximo que a empresa consegue produzir, com a atual estrutura, é 500 paletós por mês. O custo médio na produção de x paletós é igual ao quociente do custo total por x. O menor custo médio possível é igual a…
Solução (clique aqui)
(UFV-MG) Uma função f é dada por f(x) = ax + b, em que a e b são números reais. Se f(–1) = 3 e f(1) = –1, então f(3) é o número
A) 1
B) 3
C) -3
D) 5
E) -5
Solução
(UNICAMP) Considere a função afim $$f(x)=ax+b$$ definida para todo número real x , onde a e b são números reais. Sabendo que f(4)= 2 , podemos afirmar que f(f(3)+f(5)) é igual a
a) 5.
b) 4.
c) 3.
d) 2.
Solução: (clique aqui)
(ENEM) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
a) 1000
b) 1250
c) 1500
d) 2000
e) 2500
Solução: (clique aqui)
(PUC-Campinas) O gráfico a seguir representa o crescimento de uma planta durante um certo período de tempo.
Esse crescimento pode ser representado pela função f definida por
Solução
(FUVEST) Seja f a função que associa, a cada número real x, o menor dos números x + 3 e – x + 5. Assim, o valor máximo de f(x) é:
a) 1
b) 2
c) 4
d) 6
e) 7
Gabarito: c)
Solução (clique aqui)
Considere a reta r de equação dada por y=100x+(100)². Dessa forma, o número de retas de equações do tipo y=ax, com a ∈ IN, que interceptam r em pontos de coordenadas (x, y) em que x, y ∈ IN, é
igual a a) 50 b) 25 c) 75 d) 100
Gabarito: b
Solução (clique aqui)
















0 comentários